Bài toán

Trên bàn đặt một bộ bài gồm n-1 quân bài ghi lần lượt các số hiệu 1, 2 ,…, n-1, 3 £ n £10000. Trọng tài chỉ định bạn lấy k quân bài. Sau đó trọng tài đưa ra một số nguyên dương s. Bạn cần cố gắng thực hiện ít nhất m thao tác thuộc một trong hai loại + hoặc - sau đây:

+v lấy thêm quân bài số hiệu v từ trên bàn,

-vbỏ bớt quân bài số hiệu v trên tay,

để cuối cùngđạt được hệ thức

t mod n = s mod n(*)

trong đó t là tổng số hiệu các quân bài có trên tay bạn sau khi bạn đã hoàn tất m thao tác.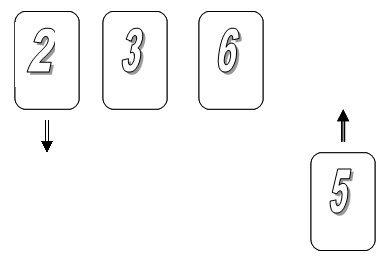

n = 8; s = 22;Trên tay giữ k = 3 quân bài 2, 3, 6.

Lời giải: Bỏ quân bài 2, lấy thêm quân bài 5.

t = 3+6+5 = 14,

t mod 8 = 14 mod 8 = 6 = s mod 8 = 22 mod 8.

Thí dụ, với n = 8, trọng tài cho số s = 22 và chỉ định bạn lấy k = 3 quân bài là 2, 3 và 6.

Nếu bạn bỏ quân bài 2 và lấy quân bài 5 thì tổng t = 3 + 6 + 5 = 14. Khi đó

t mod n = 14 mod 8 = 6 = s mod n = 22 mod 8.

Vậy một lời giải cho bộ dữ liệu này là

Thực hiện 2 thao tác: -2 và +5

Thuật toán

Ta sẽ chứng minh rằng với không quá 2 thao tác (+) lấy thêm / (-) bỏ bớt một quân bài ta có thể đạt được hệ thức (*).

Trước hết ta nhắc lại các phép toán đồng dư. Với số nguyên dương n cho trước ta xét tập các số dư trong phép chia một số tự nhiên cho n, mod n, Z_n = {0,1,2,…,n-1}. Trên Z_ncác phép toán cộng và nhân được thực hiện như bình thường sau đó lấy kết quả chia dư cho n. Phép toán lấy số đối của số x cho ta n-x. Phép trừ x-y được đổi thành phép cộng x với số đối của y. Ta có

• Cộng: (x + y) mod n
• Nhân: x*y mod n
• Lấy số đối của x: n - x
• Trừ: (x + (n-y)) mod n.

Hãy tưởng tượng các số của Z_n là 0, 1, …, n-1 được bố trí trên một vòng tròn như trên mặt đồng hồ. Để tính tổng x+y ta xuất phát từ x và di chuyển y bước theo chiều kim đồng hồ (còn gọi là di chuyển xuôi), mỗi bước ta chuyển qua một số. Kết quả sẽ là điểm dừng cuối cùng. Để tính hiệu x - y ta cũng xuất phát từ x và di chuyển y bước theo chiều ngược lại (di chuyển ngược). Để ý rằng, trên vòng tròn,di chuyển xuôi y bước sẽ cho cùng kết quả như di chuyển ngược (n-y) bước, và ngược lại, di chuyển ngược y bước sẽ tương đương như di chuyển xuôi (n-y) bước. Điều này có nghĩa là muốn thêm b đơn vị cho đại lượng t ta có thể bớt (n-b) đơn vị và ngược lại, muốn bớt b đơn vị từ đại lượng t ta có thể thêm cho t (n-b) đơn vị. Ta cũng để ý rằng số hiệu của mọi quân bài đều nhỏ thua n và mỗi quân bài hoặc là có trên tay người chơi, hoặc là nằm trên bàn. Vì lẽ trên, đôi khi người ta nói tính toán theo đồng dư (modulo) chính là tính toán trên vòng tròn.

Bạn cũng cần ghi nhớ tính chất sau đây:

Với mọi số tự nhiên x, y và n, n > 0 và với mọi phép toán số học qÎ {+, -,*} ta luôn có

(x q y) mod n = ((x mod n) q (y mod n)) mod n

Vì lũy thừa nguyên dương tương đương với phép nhân liên tiếp, ta suy ra hệ quả sau:

a^k mod n = (a mod n)^k mod n

Công thức trên cho ta quy tắc dễ hiểu sau đây: Khi tính trị của các biểu thức số học chỉ chứa các phép toán cộng, trừ và nhân trong trong Z_nta có thể thực hiện phép lấy số dư mod n trên các hạng tử và các kết quả trung gian.

Sau khi đã biết các giá trị input là n, k, s và số hiệu các quân bài cần lấy trên tay, tagán trị cho mảng a[1..n-1] như sau: a[i] = 1 cho biết quân bài i có trên tay, ngược lại, a[i] = 0 cho biết quân bài i còn nằm trên bàn. Với thí dụ đã cho, trọng tài yêu cầu ta 3 quân bài có số hiệu 2, 3 và 6 nên a = (0,1,1,0,0,1,0) ứng với a[2] = a[3] = a[6] = 1, các giá trị a[i] còn lại đều bằng 0.

Ta tính tổng số hiệu của các quân bài có trong tay lúc đầu và đặt trong biến t. Sau đó ta tính t := t mod n và s := s mod n. Với thí dụ đã cho ta tính được

t = 2+3+6 = 11, do đó t mod n = t mod 8 = 3

và s mod 8 = 22 mod 8 = 6

Tức là t = 3 và s = 6.

Giả sử t ³ s, ta đặt b = t - s và xét các trường hợp loại trừ nhau sau đây:

1.b = 0:Hệ thức (*) đã thỏa, ta không phải làm gì. Ta thông báo m = 0, trong đó m là số thao tác +/- cần thực hiện.

2.Quân bài b có trên tay, tức là a[b] = 1: Ta chỉ việc bỏ quân bài này xuống, khi đó tổng t sẽ giảm b đơn vị theo mod n.

3.Quân bài (n-b) có trên bàn, tức là a[n-b] = 0: Ta chỉ việc lấy thêm quân bài này. Khi đó tổng t sẽ được thêm (n-b) đơn vị theo mod n, điều này tương đương với việc giảm tổng t đi b đơn vị theo mod n.

4. Nếu không xảy ra các trường hợp 1, 2 và 3 như trên, tức là b ¹ 0, a[b] = 0, a[n-b]=1, ta tiến hành như sau:

Tìm hai quân bài u và v thỏa các điều kiện sau

·Quân bài u có trên tay, a[u] = 1,

·Quân bài v có trên bàn, a[v] = 0,

·u = (k*b) mod n ; v = ((k-1)*b) mod n, k là một số tự nhiên. Điều này có nghĩa là u lớn hơn v b đơn vị theo mod n.

Nếu tìm được hai quân bài u và v như trên ta sẽ thực hiện hai thao tác: bỏ quân bài u (-u) và lấy thêm quân bài v (+v). Khi đó tổng t sẽ được tăng giảm một lượngb theo mod n. Thật vậy,

(u - v) mod n = (((k*b) mod n) - (((k-1)*b) mod n)) mod n =

(k*b - (k-1)*b) mod n = b.

Trường hợp t < s ta phải thêm b = s -t đơn vị cho cho t. Việc này tương đương với giảmt bớt (n-b) đơn vị. Đặt b = n-b rồi lặp lại thủ tục trên sẽ cho ta kết quả tương ứng.

Ta chứng minh rằng nếu gặp tình huống 4 thì bao giờ cũng có thể tìm được hai quân bài u và v như đã mô tả. Trên hai ngàn năm trước nhà toán học Cổ Hylạp Diophantus đã chứng minh định lý sau:

Định lý Cho phương trình ax mod n = b mod n, với các hệ số a, b, n là các số tự nhiên, n> 0. Gọi d là ước chung lớn nhất của a và n, d = (a,n). Khi đó

a) Nếu d không là ước của b thì phương trình vô nghiệm.

b) Nếu b = kd thì phương trình có đúng d nghiệm trong tập Z_n. Các nghiệm này có dạng (x + i(n/d) ) mod n, trong đó x là một nghiệm tùy ý, i = 0,1,2...(d-1).

Phương trình ax mod n = b mod n được người đời sau gọi là phương trình Diophantus.

Chứng minh

Nếu x là nghiệm của phương trình ax mod n = b mod n thì ax vàb có cùng số dư theo mod n nên hiệu của chúng sẽ chia hết cho n, ax – b = kn, hay ax – kn = b. Mặt khác, do d = (a,n) nên a và n đều chia hết cho d và do đó ax-kn cũng chia hết cho d, thế tức là b phải chia hết cho d. Giả sử b = md tức là phương trình có nghiệm. Gọi x là nghiệm nguyên dương nhỏ nhất của phương trình trên ta dễ dàng kiểm tra được rằng x+i(n/d), i = 0,1,…,(d-1) cũng là nghiệm của phương trình đó. Thật vậy, ta để ý rằng nếu d là ước chung lớn nhất của a và n thì an/d chính là bội chung nhỏ nhất của chúng, nghĩa là an/d chia hết cho a và n. Ta có

a(x+i(n/d)) mod n = ((ax mod n) + (i(an)/d) mod n) mod n = (b mod n + 0)mod n= b mod n. Ta chứng minh xong.

Thí dụ 1. Giải phương trình sau

6x mod 9 =21 mod 9

Phương trình trên tương đương với phương trình sau:

6x mod 9 = 3

Ta có d = (6,9) = 3. Vì 3 là ước của vế phải nên phương trình đã cho có 3 nghiệm. Dễ thấy x = 2 là một nghiệm của phương trình. Vậy các nghiệm của phương trình dưới dạng tổng quat là

x + i(n/d) = 2 + i(9/3) = 2 + 3i, i = 0, 1, 2

Cụ thể là x₁ = 2, x₂ = 5 và x₃ = 8 là 3 nghiệm trong tập Z₉ = {0, 1, 2, 3, 4, 5, 6, 7, 8}.

Thí dụ 2. Giải phương trình

4x mod 12 = 5

Ta có, d = (4,12) = 4 không phải là ước của 5. Phương trình vô nghiệm.

Trở lại bài toán trên, khi gặp tình huống 4 ta có a[b] = 0 và a[n-b] = 1. Xét phương trìnhbx mod n = (n-b) mod n. Vì 1 £ b < n nên 1 £ n-b < n và do đó(n-b) mod n = n-b, phương trình đã cho có thể viết lại là bx mod n = n-b.

Theo tính chất: ước chung lớn nhất của hai số tự nhiên (a,b) sẽ không đổi nếu ta thay số lớn nhất trong hai số đó bằng hiệu của nó với số thứ hai, đặt d = (b,n), ta có d =(b,n-b), tức là n-b chia hết cho d, do đó phương trình bx mod n = n-b luôn có nghiệm. Từ nhận xét này suy rarằng vòng lặp repeat trong đoạn trình dưới đây luôn kết thúc.

u := b;

repeat

v := u;

u := (u+b) mod n;

until a[u] = 1;

Do phương trìnhbx mod n = n-b có nghiệm nên sẽ tồn tại một giá trị k để u = kb mod n = n-b. Do a[n-b] = 1 nên vòng lặp sẽ kết thúc với giá trị u=kb mod n. Vì v mang giá trị sát trước của u nên v = (k-1)b mod n.

Ta có thuật toán sau đây

1. Đọc dữ liệu vào các biến n, k và s

2. Khởi trị cho mảng a[1..n-1] với a[i] = 1 nếu quân bài i có trên tay, a[i] = 0 nếu quân bài i còn trên bàn.

3. Tính t = tổng số hiệu các quân bài có trên tay.

4. Tính t := t mod n; s := s mod n.

5. Nếu t ³ s: đặt b := t - s; ngược lại đặt b := n - (s - t).

Ý nghĩa: cần giảm b đơn vị từ tổng t để đạt hệ thức

t mod n = s mod n (*)

6. Xét các trường hợp loại trừ nhau sau đây

6.1 b = 0: Đặt m = 0; Stop.

6.2 a[b] = 1 (Quân bài b có trên tay):

Thực hiện m = 1 thao tác

-b:Bỏ quân bài b;

Stop.

6.3 a[b] = 0 và a[n-b] = 0 (Quân bài b không có trên tay, quân bài (n-b) có trên

bàn):

Thực hiện m = 1 thao tác

+(n-b):Lấy quân bài (n-b);

Stop.

6.4 a[b] = 0 và a[n-b] = 1: (Quân bài b không có trên tay, quân bài (n-b) không có

trên bàn)

6.4.1 Tính u và v

u := b;

repeat

v := u;

u := (u+b) mod n;

until a[u] = 1;

6.4.2 Thông báo: Thực hiện m = 2 thao tác

-u: Bỏ quân bài u

+v: Lấy quân bài v.

6.4.3 Stop

Từ chứng minh trên ta rút ra độ phức tạp của thuật toán là O(n) vì trong trường hợp xấu nhất ta duyệt 1 lần mảng a.

NXH

School@net