Một vài biện pháp nhằm rèn luyện năng lực vận dụng kiến thức toán học trong lập trình cho học sinh, sinh viên.

Trong thực tế giảng dạy, việc rèn luyện cho HS, SV năng lực vận dụng kiến thức toán học nhằm tìm ra TG, lựa chọn TG tối ưu đối với một BT được chúng tôi thực hiện theo quy trình sau:



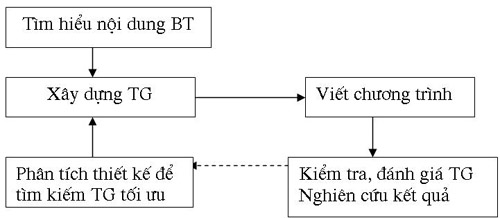
a) Hướng cho HS, SV phát hiện ra những mối liên hệ của BT cần giải quyết với các kiến thức toán thông qua quá trình tìm hiểu nội dung BT.

Nhiều BT đòi hỏi HS,SV phải tìm ra mô hình toán học cho bài toán đang được ″ẩn mình″ trong lời phát biểu ″cụ thể″ , ″rườm rà ″ của đề bài. Thực tế cho thấy những HS, SV cókhả năng vận kiến thức toán học vào quá trình phân tích đề bài sẽ nhanh chóng phát hiện được mô hình toán học của bài toán và đưa ra TG hợp lý.

Ví dụ 1: Kiểm tra một diểm M có nằm trong một một đa giác lồi P gồm n đỉnh A1,A2,...,An hay không (n ≥ 3).

+ Tương tự quá trình để tính diện tích hình thang, hình bình hành, ta phân tích đưa về bài toán đơn giản tính diện tích tam giác, ở đây ta chia đa giác P thành n tam giác (mỗi tam giác có một đỉnh là M và hai đỉnh còn lại là hai đỉnh kề nhau của tam giác) rồi tìm tổng diện tích các tam giác ấy. So sánh tổng đó với diện tích thực tế của đa giác (với sai số đủ nhỏ) ta có nhận xét: Nếu hai diện tích bằng nhau thì M nằm trong đa giác, ngược lại thì M nằm ngoài đa giác.

+ Ngoài ra, có thể đưa ra TG khác như sau: tính tổng các góc AiMAi+1 với i = 1,2,..,n và An+1 = A1. Nếu tổng đó bằng 3600thì kết luận M nằm trong , ngược lại thì kết luận M nằm ngoài đa giác

+ Tuy nhiên nếu có cái nhìn ″hình học″ hơn, ta có TG sau:

1. Tìm một điểm N nằm ngoài đa giác sao cho đường thẳng MN không đi qua đỉnh nào của đa giác.

2. Đếm số giao điểm của đoạn thẳng MN với các cạnh của đa giác.

Nếu số giao điểm đó là lẻ thì kết luận M nằm trong đa giác, ngược lại thì kết luận M nằm ngoài đa giác.

Thật vậy, nếu gọi lần lượt các giao điểm dọc theo đoạn thẳng MN với đa giác là G1, G2,..., Gm (m ≤ n). Như vậy G1G2 ε P,.., G2k-1 G2k ε P. Nên nếu M P thì m phải chẵn, từ đó suy ra nếu m lẻ thì M ε P.

b). Hình thành cho học sinh thói quen linh hoạt. sáng tạo trong việc vận dụng kiến thức toán học đã biết để đưa ra lời giải ngắn gọn, độc đáo, hợp lý nhất. Biết tận dụng kết quả ở các bước trước để giảm thao tác tính toán. Biết phân nhỏ BT thành các BT con (phương pháp chia để trị).

Ví dụ 2: Cho tam giác ABC và một điểm M không nằm trên cạnh của tam giác. Hãy viết chương trình tính số lớn nhất R sao cho vòng tròn tâm M, bán kính R không cắt bất cứ cạnh nào và không chứa tam giác ABC (Đề thi Olimpic sinh viên 2002).



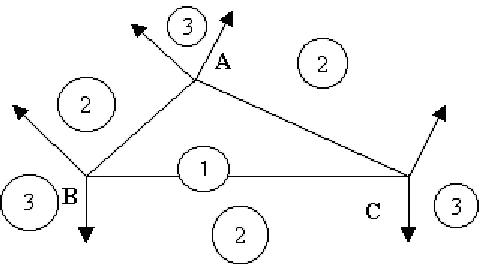
Để giải BT này, ta có thể vận dụng kiến thức của Hình học giải tích (năm thứ nhất ở bậc Đại học). Xét 3 vị trí khác nhau của điểm M so với tam giác ABC, các vị trí được phân biệt bởi các vùng được đánh dấu như hình vẽ. Ta có nhận xét:

- Nếu M thuộc vùng (1) thì

R= minimum{các khoảng cách từ M đến các cạnh của tam giác ABC}

- Nếu M nằm trong vùng (2) thì

R = khoảng cách từ M đến cạnh đối diện tương ứng;

- Các trường hợp còn lại thì

R = minimum{khoảng cách từ M đến các đỉnh của tam giác}.

Như vậy ta có TG như sau:

Bước 1: Đặt R=minimum{các khoảng cách từ M tới 3 đỉnh của tam giác}.

Bước 2: Với mỗi cạnh aiai+1,i=1,2,3 (a1 Ξ A, a2Ξ B, a3 Ξ C, a4 Ξ A), tìm toạ độ của Hi là hình chiếu của M lên cạnh aiai+1.Toạ độ của H có thể tìm được bằng cách lập phương trình đường thẳng đi qua M và vuông góc với cạnh aiai+1. Tiếp đó giải hệ phương trình của đường thẳng đó và đường thẳng đi qua ai và ai+1, nghiệm của hệ cho ta toạ độ của Hi. Gọi di là khoảng cách giữa hai điểm M và Hi, nếu d i i nằm trong đoạn thẳng a i a i+1 thì gán
R=di.

c). Chú ý cho HS, SV nghĩ đến phương án thay đổi cách nhìn BT
Trong tình huống có thể hãy chứng minh tính đúng đắn cuả TG, tìm độ phức tạp của TG nhằm giảm chi phí về thao tác cũng như bộ nhớ. Từ đó có thể lựa chọn được TG tối ưu trong số các TG khác nhau. Khi hướng đang triển khai lâm vào bế tắc, thử sử dụng kiến thức toán để chỉ ra TG không đúng, hoặc tốn kém về thời gian, bộ nhớ... Khi HS, SV vận dụng các TG kinh điển như tham lam, vét cạn, để giải BT có thể dẫn tới BT tổ hợp tìm các hoán vị của N số. Với loại bài tập này, cần phải tìm được TG tối ưu, nếu không sẽ không thể giải được trong trường hợp số N lớn. Thực vậy, chỉ với N =15 ta có : 15! =1 307 674 368 000; giả sử máy tính thực hiện với tốc độ một tỉ phép tính trên một giây và để tìm một hoán vị cần thực hiện 100 phép tính thì thời gian cần thiết để tìm hết số hoán vị trên là 130 767 giây (tức là hơn 36 giờ). Vì vậy, nếu TG đưa ra dẫn tới việc tìm các hoán vị thì cần rút lui để tìm TG khác tối ưu hơn.

Ví dụ 3: Hãy tìm cách chia số nguyên dương N (N>3) thành tổng các số tự nhiên khác nhau sao cho tích của chúng là lớn nhất. Chẳng hạn:

N= 60 được phân tích thành 2; 3; 4; 6; 7; 8; 9; 10; 11 và tích của chúng là 7983360. N= 31 được phân tích thành 2; 3; 5; 6; 7; 8 và tích của chúng là 10080.

BT này có thể giải bằng cách duyệt mọi cách chia N thành tổng các số tự nhiên. Tuy nhiên, cách làm này là ;bất khả thi; ngay cả khi N = 100 vì số phương án cần duyệt quá lớn. Vì vậy, cần phải tìm một TG tối ưu hơn. Trước hết, ta chứng minh định lý sau:

Với hai số tự nhiên a,b bất kỳ thoả mãn 1< b< a, thi` a.b>a+b.

Thật vậy: a.b>a+b <=>a.(b-1)> b <=>b-1> b/a đúng vì b-1≥1và b/a < 1.

Từ kết quả trên có thể đưa ra TG như sau: Giả sử S là tổng các số nguyên liên tiếp từ 2 cho tới K sao cho S ≥ N và K là lớn nhất có thể được. Ký hiệu T=N- S. Nếu T=0 thì các số hạng cần tìm là 2, 3,..., K, nếu T>0, chọn U là số nhỏ hơn hoặc bằng K sao cho ƯT=K+1, các số hạng cần tìm là 2,3,...,U-1, Ư1,...,K+1.

d). Rèn luyện khả năng phát hiện ra mối liên hệ giữa kiến thức toán học với BT trong TH.
Ví dụ 4: Tính số dư của phép chia BP cho M (R = BP mod M) với B và M là các số tự nhiên có không quá 12 chữ số, P là số tự nhiên không quá 3 chữ số. (Đề thi Olimpic sinh viên năm 2002)

Vì dữ liệu đầu bài cho là các số khá lớn (vượt giới hạn của dữ liệu kiểu số nguyên), nên BT có
thể giải bằng cách viết TG với số lớn với cấu trúc dữ liệu kiểu xâu (string), kiểu mảng (array) hoặc con trỏ (point). Nhưng thời gian hạn chế của phòng thi thì khó có thể cài đặt chương trình đầy đủ cho TG này. Ta có TG tối ưu hơn dựa vào công thức sau về kiến thức Số học:

Cho A, B và M là 3 số nguyên dương.

Ta có: AB mod M = (A mod M)(B mod M) mod M.

Chứng minh:

Giả sử A mod M =p1 và B mod M =p2 => A=n1M+p1và B=n2M+p2
=> AB=(n1M+p1)(n2M+p2)=(n1n2M+nư1p2+p1n2)M+p1p2
=>AB mod M = ((n1n2M+nư1p2+p1n2)M+p1p2) mod M
= p1p2 mod M
=(A mod M)(B mod M) mod M.

Dựa vào công thức trên và vận dụng một chút ;mẹo; với cấu trúc dữ liệu số thực: x mod y = x-[x/y]*y (trong đó [x/y] là ký hiệu phần nguyên của số thực x/y). Khi đó, có thể cài đặt chương trình để giải BT trên với cấu trúc dữ liệu kiểu số thực.
Rõ ràng, nếu không vận dụng kiến thức về số học thì khi gặp bài toán này, các em HSSV chỉ có thể vượt qua không quá 1/2 số test của bài.
Mặt khác, việc rèn luyện khả năng tìm ra lời giải thông qua việc vận dụng kiến thức toán học còn có tác dụng trực tiếp hay gián tiếp hình thành khả năng xây dựng TG của HS, SV.

Tài liệu tham khảo :

1. Nguyễn Bá Kim, Đinh Nho chương, Dương Mạnh Cảnh, Nguyễn Văn Thường. Phương pháp dạy học môn toán - phần 2. Giáo dục. H. 1994.

2. Tạp chí Tin học và nhà trường số 6/2002.

3. Kenneth H.Rosen. Elementary number theory and its applications, Ađison-Wesley Publishing Company, 1993.

4. Robert Sedgewick. Algorithm , Ađison-Wesley Publishing Company, 1996.

Trịnh Thanh Hải - Nguyễn