Điều này có đúng hay không? Và nếu đúng thì nó đúng trong trường hợp nào? Bài viết sau đây xin đi sâu vào phân tích kĩ những vấn đề đã nói này. Trước hết, chúng ta hãy đến với quy nạp.
I. Quy nạp
Về mặt định nghĩa, người ta cho rằng, quy nạp là kết luận đi từ trường hợp riêng đi tới trường hợp tổng quát. Nghĩa là, kết luận tổng quát dựa trên việc nghiên cứu các tính chất của nhiều sự kiện, nhiều thí nghiệm hay nhiều quan sát riêng lẻ.
Nếu kết luận chung dựa vào nghiên cứu tất cả các sự kiện riêng (các đối tượng, các hình, các số, vv…) thì quy nạp được gọi là đầy đủ hay hoàn chỉnh.
Nếu kết luận chung dựa vào nghiên cứu một phần của tâp hợp tất cả các sự kiện (các đối tượng) thì quy nạp được gọi là không đầy đủ hay không hoàn chỉnh.
Ngoài ra quy nạp còn có một số đặc trưng sau:
I.1. Quy nạp là dạng tư duy có tính phỏng đoán
Quy nạp là một dạng tư duy cực kỳ quan trọng của loài người. Hàng ngàn năm trôi qua, tư duy này đã đóng góp rất nhiều cho sự phát triển lớn lao của nhân loại. Dĩ nhiên dạng tư duy này là một dạng tư duy có tính chất dự đoán, cho nên các kết quả thu được từ việc sử dụng dạng tư duy này có thể đúng, có thể sai hoặc chưa biết. Ví dụ:
Bài toán 1. Tính tổng
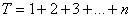
.
Dự đoán
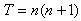
là một dự đoán đúng.
Bài toán 2.
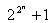
là một số nguyên tố là một dự đoán sai.
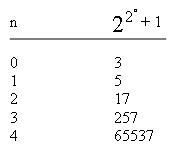
Với n đi từ 0 cho đến 5 thì theo bảng quan sát
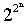
đều là số nguyên tố nhưng
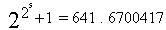
lại là hợp số.
Bài toán 3. Mọi số chẵn bắt đầu từ 4 trở lên đều có thể biểu diễn dưới dạng tổng của hai số nguyên tố.
4 = 2+ 2
6= 3+ 3
8 = 3+ 5
Dự đoán này là một dự đoán chưa có lời giải.
I.2. Quy nạp là một phương pháp giải toán
a) Cơ sở toán của nguyên lý quy nạp
Nếu W là một tính chất được xác định trên tập hợp tất cả các số tự nhiên sao cho
W(1) (1 có tính chất W)
đối với một số tự nhiên n: nếu W(n), thì W(n+1) ( nếu n có tính chất W thì n+1 có tính chất W), thì mọi số tự nhiên đều có tính chất W.
Sau đây là một số định lý quan trọng suy từ nguyên lý quy nạp.
b) Định lý 1.
Nếu W là một tính chất được xác định trong tập hợp của tất cả các số tự nhiên sao cho
W (1) (1 có tính chất W)
đối với mọi số tự nhiên n: nếu W(k) (k có tính chất W) với mọi số tự nhiên k: sao cho thì W(n+1) (n+1 có tính chất W),
thì mọi số tự nhiên đều có tính chất W.
c) Định lý 2.
Nếu là hàm mệnh đề của biến x biến thiên trên tập hợp tất cả các số tự nhiên sao cho
(1) (1 thoả mãn mệnh đề φ(x))
đối với mọi số tự nhiên n: nếu (k) (k thoả mãn (x)) đối với mọi số tự nhiên k sao cho , thì φ(n+1) (n+1 thỏa mãn φ(x)),
thì mọi số tự nhiên thỏa mãn hàm mệnh đề φ(x).
d) Một số áp dụng.
Bài toán 4.
Đối với một số tự nhiên n, số tất cả các tập hợp con của một tập hợp có n phần tử thì bằng
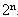
.
Chứng minh.
Gọi W là một tính chất của số tự nhiên sao cho W(n) khi và chỉ khi số tất cả các tập hợp con của một tập hợp có n phần tử bằng
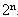
. Ta thấy rằng:
Số 1 có tính chất W (*)
Gọi
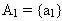
thì tập hợp có hai tập con {Φ} và tập hợp
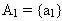
. Vậy số tất cả các tập hợp con của tập hợp có một phần tử bằng:
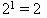
Ta sẽ chứng minh: nếu một số tự nhiên n có tính chất W thì n+1 có tính chất W. (**)
Để làm điều đó, ta giả sử rằng số n có tính chất W. Bây giơ, xét một tập hợp bất kì có n+1 phần tử
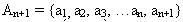
. Ta chia tất cả các tập hợp con của tập hợp đó thành hai họ. Họ thứ nhất sẽ gồm mọi tập hợp con không chứa các phần tử
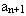
còn họ thứ hai gồm mọi tập hợp con chứa
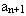
. Hai họ này rời nhau và hợp của chúng là họ tất cả các tập hợp con của tập hợp An+1. Họ thứ nhất gồm tất cả các tập hợp con của tập hợp
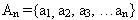
của n phần tử và không chứa bất kỳ một tập hợp nào khác. Vì theo giả thiết n có tính chất W nên họ thứ nhất chứa đúng
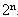
tập hợp. Các tập hợp của họ thứ hai có được từ những tập hợp của họ thứ nhất khi thêm vào phần tử
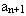
. Họ thứ hai có số tập hợp nhiều như số các tập hợp con của họ thứ nhất, tức là bằng
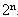
.
Do đó, số tất cả các tập hợp con của
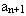
bằng
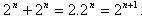
. Ta kết luận: số n+1 có tính W. Điều này chứng minh (**).
Vậy theo nguyên lý quy nạp, ta có đối với mọi số tự nhiên n, số tất cả các tập hợp con của một tập hợp có n phần tử thì bằng 2n.
Lẽ dĩ nhiên, ta còn có lý thuyết tổng quát về quy nạp. Nhưng ta sẽ không trình bày kĩ ở đây. Bước tiếp theo, ta sẽ tìm hiểu về đệ quy.
II. Đệ quy
Về mặt toán học, người ta nghiên cứu một dãy hàm có dạng y = f(x1, x2, …, xn) mà giá trị đối số của nó là các số nguyên không âm và với chúng có thể chỉ ra những quy tắc xác định, cho phép thực tế tính được y theo bộ x1, x2, …, xn cho trước trong miền xác định của hàm f. Người ta cũng đã coi khái niệm hàm đệ quy bộ phận là các hàm mà có thể tính được bằng thuật toán. Lý thuyết hàm đệ quy còn được dùng nhiều trong các máy tính điện tử hiện đại ngày nay. Và nó đã trở thành một lĩnh vực nghiên cứu riêng của toán học từ những năm 1940.
Về mặt tin học, người ta rất chú trọng đến phương pháp đệ quy. Nó là một công cụ được thường xuyên sử dụng trong lập trình. Để giải quyết một bài toán hay một vấn đề nào đó mà sử dụng được đệ quy, người ta tiến hành qua hai bước bước phân tích và bước thế ngược.
Do đó bài toán giải theo phương pháp đệ quy phải cần hai điều kiện sau đây để có được tính đệ quy và để không bị gọi đệ quy bất tận :
1). Để có được tính đệ quy, nghĩa là để giải một bài toán chúng ta cần phải giải bài toán đồng dạng (đơn giản hơn, để giải bài toán đồng dạng này chúng ta phải giải bài toán đồng dạng khác( đơn giản hơn nữa). Vì vậy, phải tồn tại bước đệ quy. Ví dụ với bài toán tính giai thừa:
Bài toán 5: Tính giai thừa n! = 1x2x3…n có thuật toán:
function Giaithua (n : integer) : integer;
begin
if (n = 0) then
Giaithua:=1
else
Giaithua:= n* Giaithua (n-1)
end;
Với các khẳng định đầu vào và đầu ra
Input: n là số nguyên không âm
Output: Giá trị của hàm là n!
có bước đệ quy là Giaithua(n) : = n * Giaithua(n-1)
2). Để không bị gọi đệ quy bất tận thì phải có điều kiện dừng. Bài toán tính giai thừa có điều kiện dừng là Giaithua (1) : = 1.
Thêm vào đó, người ta phân đệ quy ra làm hai loại : đệ quy trực tiếp và đệ quy gián tiếp. Thông thường chúng ta làm việc với đệ quy trực tiếp. Tuy nhiên cũng có lúc ta làm việc với đệ quy gián tiếp. Phép đệ quy gián tiếp xảy ra khi một chương trình con gọi các chương trình con khác, và một dãy nào đó các tham trỏ của chương trình con cuối cùng sẽ tham trỏ đến chương trình con đầu tiên. Tuỳ theo ngôn ngữ lập trình, người ta có xử lý riêng cho loại đệ quy này.
III. So sánh quy nạp với đệ quy
III.1. Quy nạp với vai trò là tư duy
Do môi trường làm việc của toán và tin có sự khác biệt cho nên phương pháp quy nạp và phương pháp đệ quy cũng không hề giống nhau.
1). Quy nạp là một loại tư duy có tính phỏng đoán. Cho nên những kết quả có được khi sử dụng quy nạp có thể đúng, sai hoặc chưa biết đúng hay sai (Do nó dựa trên sự quan sát từ những trường hợp riêng lẻ để đi đến trường hợp tổng quát). Trong khi đệ quy không có được những tính chất đó của quy nạp.
III.2. Quy nạp với vai trò là phương pháp chứng minh
2). Phép quy nạp chứng minh được trường hợp tổng quát của một số các bài toán trong khi đệ quy thì không. Bởi lẽ, quy nạp toán học là một phương pháp thường dùng mà đi từ việc xác định bài toán có tính chất W(1) cộng với giả sử bài toán có tính chất W(n) (Với mọi số tự nhiên n) rồi chứng minh được bài toán cũng có tính chất W(n+1) thì ta kết luận bài toán có tính chất W với mọi số tự nhiên (xem I.2.a)
3). Quy nạp có thể tham gia vào chứng minh tính đúng đắn các thuật toán đệ quy. Ví dụ như trong giải thuật giai thừa nói trên, bằng phương pháp quy nạp, ta có thể chỉ ra rằng khẳng định đầu ra Output được kéo theo từ khẳng định đầu vào Input. Nếu n = 0, lệnh tương ứng của nó sẽ là :
Giaithua :=1 (điều kiện dừng)
lập tức được thực hiện. Thuật toán kết thúc và giá tri đúng của hàm là 0! được trả. Giả sử rằng với số nguyên k không âm, hàm kết thúc với n = k và trả giá trị đúng k!. Khi hàm được tham trỏ với tham số n=k+1, lệnh quy nạp:
Giaithua : = n * Giaithua (n -1)
được thực hiện. Giá trị của n - 1 là k. Vì vậy, theo giả thiết quy nạp, tham trỏ Giaithua(n - 1) kết thúc và cho giá trị đúng là k!. Từ đó suy ra rằng, tham trỏ với tham số n = k+1 cũng kết thúc và cho giá trị đúng là (k + 1) * k! = (k + 1)!. Như vậy, chúng ta đã chứng minh được rằng, trong mọi trường hợp khẳng định đầu ra được kéo theo từ khẳng định đầu vào.
4). Ở một số bài toán, chúng ta không thể sử dụng phương pháp quy nạp mà chỉ có thể sử dụng phương pháp đệ quy.
Vấn đề này đã được Afred V. Aho và Jeffrey D. Allman chỉ rõ:
"Thường thì người ta cố gắng thực hiện quy nạp trên số nút của cây, trong đó chúng ta giả thiết một khẳng định cho các cây có n nút và chứng minh điều đó cho cây có n + 1 nút. Đây là một chứng minh sai lầm nếu chúng ta không cẩn thận" "Chúng ta đã đề xuất một phương pháp luận thích hợp, trong đó chúng ta cố gắng chứng minh khẳng định S(n+1) bằng cách dùng S(n); gọi cách tiếp cận này là phương pháp tựa lưng. Đôi khi chúng ta muốn xem quá trình này như khởi đầu với S(n) và chứng minh S(n+1); gọi cách tiếp cận này là "nới rộng". Trong trường hợp số nguyên, chúng là những ý tưởng giống nhau. Tuy nhiên với các cây, chúng ta không thể bắt đầu bằng cách giả sử khẳng định đúng cho cây n nút, thêm một nút vào một vị trí nào đó và khẳng định kết quả được chứng minh cho tất cả mọi cây (n +1) nút.
Thí dụ xét khẳng định S(n): "Tất cả mọi cây n nút đều có một đường đi có chiều dài n - 1". Điều này chắc chắn đúng với cơ sở n = 1. Bằng một qui nạp sai lầm, chúng ta lập luận "Giả sử một cây T với n nút có một đường đi dài n - 1, chẳng hạn đường đi đến một nút v. Thêm một con u cho v. Bây giờ chúng ta có một cây (n +1) nút với chiều dài n, chứng minh bước qui nạp".
Dĩ nhiên lập luận này là sai lầm bởi nó không chứng minh kết quả cho tất cả các cây (n + 1) nút mà chỉ là cho các cây đã được chọn. Một chứng minh đúng đắn không "nới rộng" từ n sang (n+1) nút bởi vì như thế chúng ta không bao quát được hết tất cả các cây có thể có. Đúng ra phải sử dụng "tựa lưng" bằng cách khởi đầu với một cây có (n + 1) nút rồi chọn lựa cẩn thận một nút để loại bỏ, thu được một cây n nút." (Alfred V.Aho, Jeffrey D. Ullman, Cơ sở của khoa học máy tính, An bản C, Tập 2, Nhà Xất Bản Thống Kê, 1999, Tr. 327)
5). Lời giải quy nạp ở một số bài toán có tính chất tương tự trong khi đệ quy thì không.
Bài toán 6:
Đối với mọi số tự nhiên n và k <= n thì số tất cả các tổ hợp của k phân tử lấy từ những phần tử của một tập hợp n phần tử thì bằng
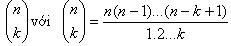
.
Có lời giải bằng phương pháp quy nạp:
Cho W là một tính chất của các số tự nhiên sao cho W(n) khi và chỉ khi số tất cả các tổ hợp của k phần tử, lấy từ những phần tử của một tập hợp n phần tử thì bằng
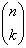
. Ta phải chứng minh rằng: 1 có tính chất W.
Nếu n = 1 thì k chỉ có thể bằng 1. Số tất cả các tổ hợp của một phần tử lấy từ các phần tử của một tập hợp có một phần tử sẽ bằng 1. Như vậy
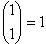
, Vậy 1 có tính chất W.
Ta phải chứng minh rằng nếu n có tính chất W thì n + 1 có tính chất W.
Để chứng minh điều này ta phải giả sử rằng một số tự nhiên n có tính chất W. Xét một tập hợp bất kì của n + 1 phần tử
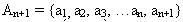
và lập tất cả các tổ hợp 1 phần tử. Số các tổ hợp ấy rõ ràng bằng
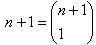
. Cũng cần chú ý rằng số tất cả các tổ hợp của n+1 phần tử lấy từ các phần tử của An+1 thì bằng
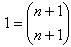
. Gọi k là số tự nhiên bất kỳ sao cho 1 < k < n+1. Bây giờ, ta lập tất cả các tổ hợp k phần tử lấy từ những phần tử của An+1, tức là các tập hợp con mà mỗi tập hợp có k phần tử và chia chúng thành hai họ các tập hợp. Họ thứ nhất gồm mọi tập hợp con của An+1 có k phần tử có chứa an+1 . Họ thứ hai sẽ chứa tất cả các tập hợp con của An+1 không chứa an+1.
Các họ này rời xa nhau và hợp của chúng là họ tất cả các tập hợp con của
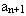
có k phần tử. Họ thứ nhất sẽ có số tập hợp nhiều bằng số tập hợp con của k-1 phần tử có thể lập ra được từ tập hợp của n phần tử. Vì theo giả thiết n có tính chất W nên có thể lập được
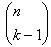
những tập hợp con ấy. Họ thứ hai có số tập hợp nhiều bằng số các tập hợp con gồm k phần tử có thể lập được từ tập hợp của n phần tử, tức là
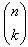
vì n có tính chất W. Số tất cả các tập hợp của k phần tử được lập ra những phần tử của
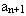
là tổng số các tập hợp thuộc họ thứ nhất và số các tập hợp thuộc họ thứ hai và do
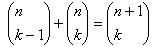
với n>1, n ≥k>1 (***). Sở dĩ có được (***) là vì:
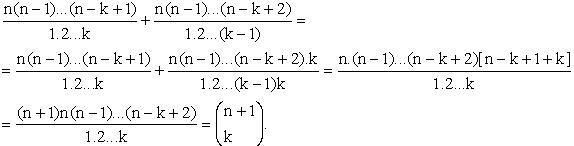
Chúng ta đã chứng minh được rằng với mọi , số tất cả các tổ hợp k phần tử lập từ các phần tử của
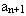
thì bằng
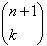
và do đó n + 1 có tính chất W. Như vậy ta đã hoàn toàn chứng minh được bài toán 6.
Lời giải bằng phương pháp đệ quy của bài toán này và lời giải bằng phương pháp đệ quy của bài toán 4 là tương tự nhau. Bởi chúng dựa trên lập luận phân tập hợp
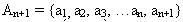
thành hai họ tập hợp. Rồi sau đó dựa vào giả thiết quy nạp n có tính chất W để từ đó rút ra n + 1 cũng có tính chất W.
Có một điều dáng chú ý rằng, bài toán 4 và bài toán 6 có lời giải bằng phương pháp quy nạp tương tự nhau thì lời giải đệ quy lại không có tác dụng gì ở đây. Ta khó có thể sử dụng được phương pháp đệ quy cho việc chứng minh các bài toán có tính trừu tượng như thế này.
6). Lời giải đệ quy ở một số bài toán có tính tương tự trong khi lời giải quy nạp thì không. Một số ví dụ minh hoạ cho nó đó là thuật toán đệ quy tính n! ở bài toán 5 và thuật toán đệ quy cho việc tính tổng ở bài toán 1:
function Sum(n : integer) : integer;
begin
if (n = 1) then
Sum : = 1
else
Sum : = n + Sum ( n-1)
end;
là tương tự nhau, trong khi nếu ta sử dụng phương pháp quy nạp thì rõ ràng ta chỉ sử dụng được nó cho bài toán tính tổng 1 + 2 + … + n mà thôi còn tính giai thừa thì ta không thể làm được. Bởi lẽ không có một công thức tổng quát nào của n! để ta có thể thực hiện được phương pháp quy nạp cho nó.
7). Chúng ta không thể sử dung phương pháp đệ quy ở một số bài toán mà chỉ có thể sử dụng quy nạp. Ví dụ bài toán 4 và bài toán 6, ta chỉ có thể thực hiện được phương pháp quy nạp.
Qua những điều tìm hiểu đặc biệt là bảy bước so sánh mà ta vừa nói ở trên, ta thấy rõ một điều, đệ quy và quy nạp có sự khác biệt rõ rệt bởi bản chất của đệ quy và quy nạp về mặt phương pháp, về mặt khái niệm, về mặt tư duy, về mặt ứng dụng có sự khác biệt cũng như môi trường làm việc của toán và tin không hề giống nhau. Những điều này nếu ta không nắm kỹ thì sẽ dẫn đến sai lầm chủ quan. Ngay cả những bậc thầy về lập trình như Larry Nyhoff và Sanford Leedsma, tác giả của những cuốn sách gối đầu giường cho bao thế hệ sinh viên lập trình, tôi e, cũng đã mắc phải sai lầm khi cho rằng :
"Phép quy nạp toán học cũng rất có ích cho việc chứng minh tính đúng đắn của các thuật toán đệ quy do bản chất của nó là phép đệ quy đòi hỏi phép quy nạp" (Larry Nyhoff - Sanford Leedstma, lập trình nâng cao bằng Pascal với các cấu trúc dữ liệu, Tập 1, Nhà xuất bản Đà Nẵng, 1997, Tr. 192).
Một lần nữa tôi xin được nhấn mạnh một điều rằng, chúng ta không nên chỉ quan tâm vào hình thức của một vấn đề nào đó, không nên chỉ quan sát vào một số trường hợp cá thể mà phải đi sâu vào tìm hiểu bản chất của nó để từ đó mới có thể rút ra được kết luận đúng đắn. Nếu không chúng ta sẽ dễ dẫn đến những kết quả quy nạp không hoàn toàn. Và nếu vấn đề của chúng ta gặp phải là sự so sánh giữa toán và tin thì chúng ta cần phải có thêm một cách nhìn đầy đủ ở cả hai lĩnh vực. Điều đó giúp chúng ta đánh giá được vấn đề một cách chính xác nhất và toàn diện nhất.

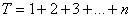 .
.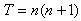 là một dự đoán đúng.
là một dự đoán đúng.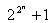 là một số nguyên tố là một dự đoán sai.
là một số nguyên tố là một dự đoán sai.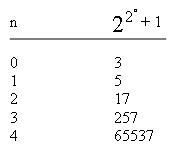
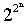 đều là số nguyên tố nhưng
đều là số nguyên tố nhưng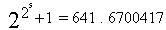 lại là hợp số.
lại là hợp số.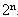 .
. 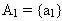 thì tập hợp có hai tập con {Φ} và tập hợp
thì tập hợp có hai tập con {Φ} và tập hợp 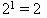
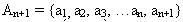 . Ta chia tất cả các tập hợp con của tập hợp đó thành hai họ. Họ thứ nhất sẽ gồm mọi tập hợp con không chứa các phần tử
. Ta chia tất cả các tập hợp con của tập hợp đó thành hai họ. Họ thứ nhất sẽ gồm mọi tập hợp con không chứa các phần tử 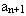 còn họ thứ hai gồm mọi tập hợp con chứa
còn họ thứ hai gồm mọi tập hợp con chứa 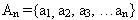 của n phần tử và không chứa bất kỳ một tập hợp nào khác. Vì theo giả thiết n có tính chất W nên họ thứ nhất chứa đúng
của n phần tử và không chứa bất kỳ một tập hợp nào khác. Vì theo giả thiết n có tính chất W nên họ thứ nhất chứa đúng 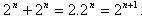 . Ta kết luận: số n+1 có tính W. Điều này chứng minh (**).
. Ta kết luận: số n+1 có tính W. Điều này chứng minh (**).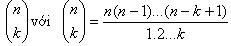 .
.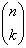 . Ta phải chứng minh rằng: 1 có tính chất W.
. Ta phải chứng minh rằng: 1 có tính chất W.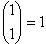 , Vậy 1 có tính chất W.
, Vậy 1 có tính chất W.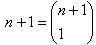 . Cũng cần chú ý rằng số tất cả các tổ hợp của n+1 phần tử lấy từ các phần tử của An+1 thì bằng
. Cũng cần chú ý rằng số tất cả các tổ hợp của n+1 phần tử lấy từ các phần tử của An+1 thì bằng 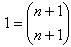 . Gọi k là số tự nhiên bất kỳ sao cho 1 < k < n+1. Bây giờ, ta lập tất cả các tổ hợp k phần tử lấy từ những phần tử của An+1, tức là các tập hợp con mà mỗi tập hợp có k phần tử và chia chúng thành hai họ các tập hợp. Họ thứ nhất gồm mọi tập hợp con của An+1 có k phần tử có chứa an+1 . Họ thứ hai sẽ chứa tất cả các tập hợp con của An+1 không chứa an+1.
. Gọi k là số tự nhiên bất kỳ sao cho 1 < k < n+1. Bây giờ, ta lập tất cả các tổ hợp k phần tử lấy từ những phần tử của An+1, tức là các tập hợp con mà mỗi tập hợp có k phần tử và chia chúng thành hai họ các tập hợp. Họ thứ nhất gồm mọi tập hợp con của An+1 có k phần tử có chứa an+1 . Họ thứ hai sẽ chứa tất cả các tập hợp con của An+1 không chứa an+1. 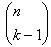 những tập hợp con ấy. Họ thứ hai có số tập hợp nhiều bằng số các tập hợp con gồm k phần tử có thể lập được từ tập hợp của n phần tử, tức là
những tập hợp con ấy. Họ thứ hai có số tập hợp nhiều bằng số các tập hợp con gồm k phần tử có thể lập được từ tập hợp của n phần tử, tức là 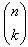 vì n có tính chất W. Số tất cả các tập hợp của k phần tử được lập ra những phần tử của
vì n có tính chất W. Số tất cả các tập hợp của k phần tử được lập ra những phần tử của 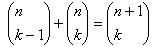 với n>1, n ≥k>1 (***). Sở dĩ có được (***) là vì:
với n>1, n ≥k>1 (***). Sở dĩ có được (***) là vì: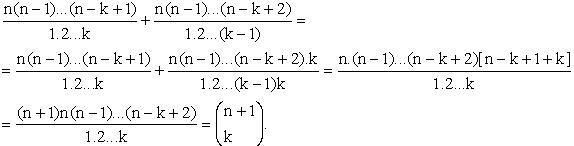
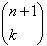 và do đó n + 1 có tính chất W. Như vậy ta đã hoàn toàn chứng minh được bài toán 6.
và do đó n + 1 có tính chất W. Như vậy ta đã hoàn toàn chứng minh được bài toán 6.

