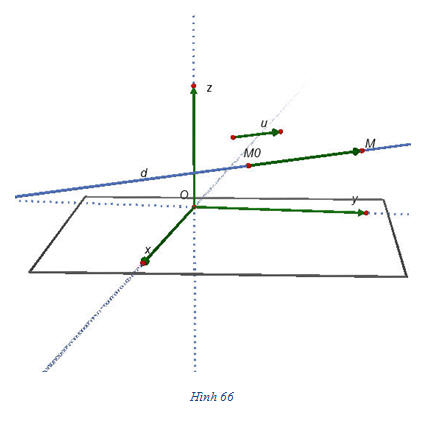
Tải trực tiếp tệp hình học động (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h66.cg3 Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Ta biết rằng điều kiện cần và đủ để điểm nằm trên đường thẳng d là vectơ 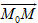 cùng phương với vectơ cùng phương với vectơ 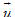 , tức là có số , tức là có số 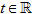 sao cho sao cho 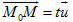 . Chú ý rằng . Chú ý rằng 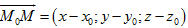 nên điều kiện nói trên tương đương với: nên điều kiện nói trên tương đương với: 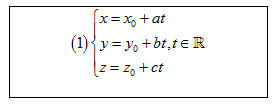
Hệ phương trình (1) được gọi là phương trình tham số của đường thẳng d với tham số t. Với mỗi 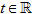 , hệ phương trình trên cho ta tọa độ (x; y; z) của một điểm nằm trên d. , hệ phương trình trên cho ta tọa độ (x; y; z) của một điểm nằm trên d. Ngược lại, mỗi hệ phương trình dạng (1) với a2 + b2 + c2 > 0 đều là phương trình tham số của đường thẳng d đi qua điểm (x0; y0; z0) và có vectơ chỉ phương là 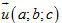 . . Từ nay, để đơn giản, trong phương trình (1) ta không viết 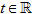 . .  1 Cho đường thẳng d có phương trình tham số: 1 Cho đường thẳng d có phương trình tham số:
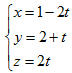
a) Hãy tìm tọa độ của một vectơ chỉ phương của d. b) Xác định tọa độ của các điểm thuộc d ứng với giá trị t = 0, t = 1, t = -2.. c) Trong các điểm A(3; 1; -2), B(-3; 4; 2), C(0; 2; 5; 1), điểm nào thuộc d, điểm nào không? Xét đường thẳng d có phương trình tham số (1). Trong trường hợp abc , bằng cách khử t từ các phương trình của hệ (1) ta được: 
Hệ phương trình (2) được gọi là phương trình chính tắc của đường thẳng d. Ngược lại, mỗi hệ phương trình như thế đều là phương trình chính tắc của một đường thẳng hoàn toàn xác định, đó là đường thẳng đi qua điểm (x0; y0; z0) và có một vectơ chỉ phương là 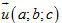 . .  2 Cho hai mặt phẳng 2 Cho hai mặt phẳng 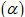 và và 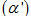 có phương trình: có phương trình:
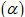 : 2x + 2y + z - 4 = 0 : 2x + 2y + z - 4 = 0
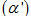 : 2x - y - z + 5 = 0 : 2x - y - z + 5 = 0
a) Hãy giải thích tại sao hai mặt phẳng 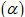 và và 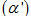 cắt nhau. cắt nhau. b) Gọi d là giao tuyến của hai mặt phẳng 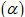 và và 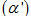 . Hãy tìm tọa độ của một điểm thuộc d và xác định tọa độ của một vectơ chỉ phương của d. . Hãy tìm tọa độ của một điểm thuộc d và xác định tọa độ của một vectơ chỉ phương của d. c) Viết phương trình tham số và chính tắc của đường thẳng d. 2. Một số ví dụ Ví dụ 1. Viết phương trình tham số của đường thẳng d đi qua hai điểm phân biệt A(1; 0; -2) và (2; 1; 1). Giải Vectơ 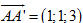 là một vectơ chỉ phương của d, ngoài ra d đi qua điểm A nên d có phương trình tham số là là một vectơ chỉ phương của d, ngoài ra d đi qua điểm A nên d có phương trình tham số là 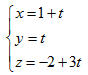
Ví dụ 2. Trong không gian tọa độ Oxyz, cho tứ diện ABCD với A = ( 0 ; 0 ; 2 ) , B = ( 3 ; 0 ; 5 ) , C = ( 1 ; 1 ; 0 ) , D = ( 4 ; 1 ; 2 ). a) Viết phương trình tham số của đường cao tứ diện ABCD hạ từ D. b) Tìm tọa độ hình chiếu H của D trên mặt phẳng (ABC). Giải a) Ta có 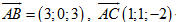 . . Vì 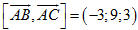 nên một vectơ pháp tuyến của mặt phẳng (ABC) là nên một vectơ pháp tuyến của mặt phẳng (ABC) là 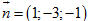 . . Vậy phương trình tham số của đường cao d hạ từ D của tứ diện là 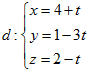
b) Mặt phẳng (ABC) có vectơ pháp tuyến 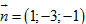 và đi qua A(0 ; 0 ; 2) nên có phương trình là và đi qua A(0 ; 0 ; 2) nên có phương trình là 1(x - 0) - 3(y - 0) - 1(z - 2) = 0 hay x - 3y - z + 2 = 0. Hình chiếu H của D trên mặt phẳng (ABC) là giao điểm của đường thẳng d với mặt phẳng (ABC). Để tìm tọa độ điểm H, ta giải hệ gồm các phương trình của đường thẳng d và mp(ABC). 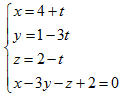
Thay các giá trị của x, y, z trong ba phương trình đầu vào phương trình cuối, ta có 4 + t - 3(1 - 3t) - (2 - t) + 2 = 0. Từ đó suy ra: 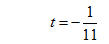
Do đó 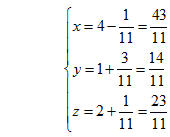
Vậy 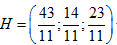
Ví dụ 3. Cho hai mặt phẳng 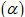 và và 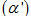 lần lượt có phương trình lần lượt có phương trình x + 2y - z + 1 = 0 và x + y + 2z + 3 = 0. Chứng tỏ rằng hai mặt phẳng đó cắt nhau và viết phương trình tham số của giao tuyến hai mặt phẳng đó. Giải Hai mặt phẳng đã cho cắt nhau vì bộ ba số (1; 2; -1) không tỉ lệ với bộ ba số (1; 1; 2). Gọi d là đường thẳng giao tuyến của chúng. Đường thẳng d gồm các điểm M(x; y; z) vừa thuộc 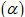 vừa thuộc vừa thuộc 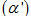 nên tọa độ của M là nghiệm của hệ: nên tọa độ của M là nghiệm của hệ: 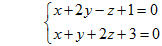
Bây giờ ta có thể viết phương trình tham số của d bằng một trong các cách sau đây: Cách 1. Tìm tọa độ một điểm A thuộc d và một vectơ chỉ phương của nó rồi viết phương trình tham số của d. Cụ thể là, trong hệ (1) cho z = 0 rồi tìm x và y, ta được x = -5 , y = 2. Vậy điểm A(-5; 2; 0) thuộc d. Gọi  là vectơ pháp tuyến của mặt phẳng là vectơ pháp tuyến của mặt phẳng 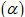 , ,  là vectơ pháp tuyến của mặt phẳng là vectơ pháp tuyến của mặt phẳng 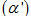 . Đường thẳng d vuông góc với . Đường thẳng d vuông góc với  và và  nên nó có vectơ chỉ phương là nên nó có vectơ chỉ phương là  . . Vậy, phương trình tham số của đường thẳng d là 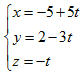
Cách 2. Tìm tọa độ hai điểm phân biệt A và A’ thuộc d rồi viết phương trình đường thẳng đi qua hai điểm đó. Cụ thể là: Trong hệ (1) cho z = 0, ta tìm được x = -5, y = 2. Vậy điểm A(-5; 2; 0) thuộc d. Lại cho z = 1, ta được x = -10, y = 5. Vậy A’(-10; 5; 1) cũng thuộc d. Vectơ chỉ phương của d là  nên d có phương trình tham số là: nên d có phương trình tham số là: 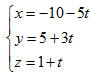
Cách 3. Trong hệ (1) cho z = t rồi tìm x và y theo t, ta được 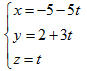
Đó cũng là phương trình tham số của đường thẳng d. Ví dụ 4. Cho hai đường thẳng d1và d2 lần lượt có phương trình là 
Viết phương trình chính tắc của đường thẳng d3 đi qua điểm M(1; -1; 2), vuông góc với cả d1 và d2. Giải Các đường thẳng d1 và d2 lần lượt có vectơ chỉ phương là 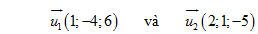
Đường thẳng d3 vuông góc với cả d1 và d2 nên một vectơ chỉ phương của d3 là  . Ta tính được . Ta tính được  và do đó d3 có phương trình chính tắc là và do đó d3 có phương trình chính tắc là 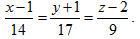 3. Vị trí tương đối giữa hai đường thẳng Trong không gian, cho đường thẳng d đi qua điểm M0, có vectơ chỉ phương 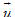 và đường thẳng d’ đi qua điểm M’0, có vectơ chỉ phương và đường thẳng d’ đi qua điểm M’0, có vectơ chỉ phương 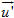 . Dựa vào vectơ . Dựa vào vectơ 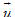 , , 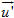 và và 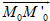 , ta có thể biết được vị trí tương đối giữa hai đường thẳng d và d’. , ta có thể biết được vị trí tương đối giữa hai đường thẳng d và d’. 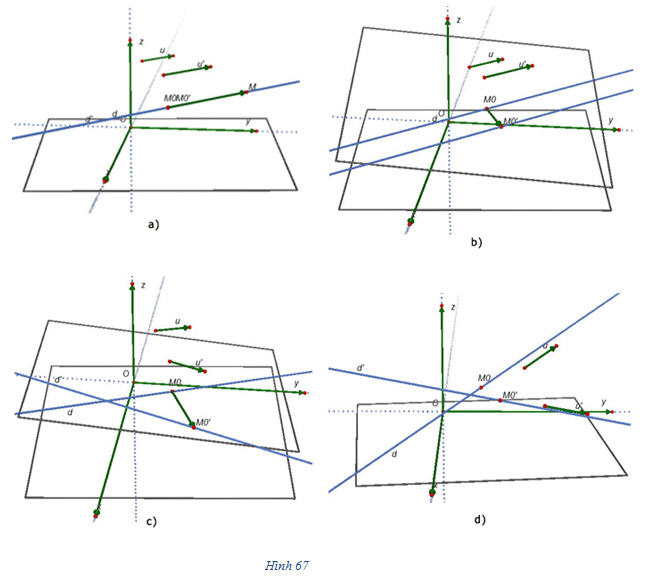
Tải trực tiếp tệp hình học động 67a (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h67a.cg3
Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tải trực tiếp tệp hình học động 67b (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h67b.cg3
Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tải trực tiếp tệp hình học động 67c (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h67c.cg3
Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe )
Tải trực tiếp tệp hình học động 67d (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h67d.cg3
Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Cụ thể là: a) d và d’ trùng nhau khi và chỉ khi ba vectơ 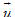 , , 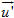 và và 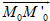 đôi một cùng phương (h.67a). đôi một cùng phương (h.67a). b) d // d’ khi và chỉ khi 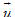 và và 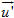 cùng phương nhưng không cùng phương với cùng phương nhưng không cùng phương với 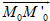 (h.67b). (h.67b). c) d và d’ cắt nhau khi và chỉ khi 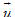 và và 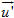 không cùng phương, đồng thời ba vectơ không cùng phương, đồng thời ba vectơ 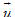 , , 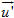 và và 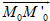 đồng phẳng (h.67c). đồng phẳng (h.67c). d) d và d’ chéo nhau khi và chỉ khi d, d’ không đồng phẳng, hay khi và chỉ khi ba vectơ 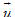 , , 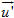 và và 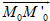 không đồng phẳng (h.67d). không đồng phẳng (h.67d). Vậy ta có: 
 Khi nào hai đường thẳng d và d’ nói trên vuông góc với nhau? Khi nào hai đường thẳng d và d’ nói trên vuông góc với nhau?
Ví dụ 5. Trong không gian Oxyz, xét cặp đường thẳng dm, d’m có phương trình 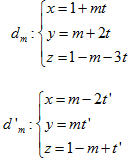
Xác định vị trí tương đối giữa hai đường thẳng đó tùy theo giá trị của m. Giải Đường thẳng dm đi qua điểm M(1; m; 1 - m) và có vectơ chỉ phương  . Đường thẳng d’m đi qua điểm M’(m; 0; 1 - m) và có vectơ chỉ phương là . Đường thẳng d’m đi qua điểm M’(m; 0; 1 - m) và có vectơ chỉ phương là  . . Ta có  . . Từ đó ta tính được 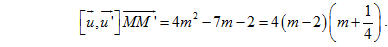
Vậy: Nếu m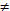 2 và m 2 và m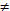 - 1/4 thì hai đường thẳng đã cho chéo nhau ; - 1/4 thì hai đường thẳng đã cho chéo nhau ; Nếu thì  và và  không cùng phương, suy ra hai đường thẳng đã cho cắt nhau; không cùng phương, suy ra hai đường thẳng đã cho cắt nhau; Nếu m = -1/4 thì  và và  cũng không cùng phương, suy ra hai đường thẳng đã cho cắt nhau. cũng không cùng phương, suy ra hai đường thẳng đã cho cắt nhau. CHÚ Ý Nếu biết phương trình của hai đường thẳng d và d’ thì ta cũng có thể xét vị trí tương đối giữa chúng bằng cách giải hệ gồm các phương trình xác định d và d’ để tìm giao điểm. Nếu hệ phương trình có nghiệm duy nhất thì d và d’ cắt nhau. Nếu hệ phương trình có vô số nghiệm thì d và d’ trùng nhau. Nếu hệ phương trình vô nghiệm thì d và d’ song song hoặc chéo nhau, song song nếu hai vectơ chỉ phương của chúng cùng phương, chéo nhau nếu hai vectơ đó không cùng phương. Ví dụ 6. Cho đường thẳng d là giao tuyến của hai mặt phẳng 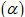 : x + y = 0 : x + y = 0
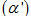 : 2x - y + z - 15 = 0 : 2x - y + z - 15 = 0
và đường thẳng d’ có phương trình 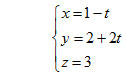
Xác định vị trí tương đối giữa hai đường thẳng d và d’. Giải Cách 1 Trong hệ gồm hai phương trình của hai mặt phẳng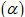 và và 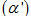 , ta cho thì và . Vậy điểm M(0 ; 0; 15) nằm trên d. , ta cho thì và . Vậy điểm M(0 ; 0; 15) nằm trên d. Lại cho x = 1 thì y = -1 và z = 12. Vậy điểm N(1; -1; 12) nằm trên d. Như vậy d là đường thẳng đi qua M và có vectơ chỉ phương 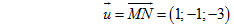
Đường thẳng d’ đi qua M’(1; 2; 3) và có vectơ chỉ phương 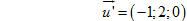
Ta có  . . Dễ thấy rằng  , tức là ba vectơ , tức là ba vectơ  đồng phẳng. đồng phẳng. Ngoài ra hai vectơ  không cùng phương. không cùng phương. Từ đó suy ra hai đường thẳng d và d’ cắt nhau. Cách 2 Mặt phẳng 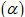 có vectơ pháp tuyến là có vectơ pháp tuyến là  . . Mặt phẳng 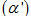 có vectơ pháp tuyến là có vectơ pháp tuyến là  . . Do đó, vectơ chỉ phương của d là  . . Đường thẳng d’ có vectơ chỉ phương là  . . 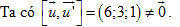
Mặt khác, điểm M0(0; 0; 15)  d, điểm M’0(1; 2; 3) d, điểm M’0(1; 2; 3)  d’, d’, 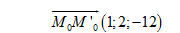
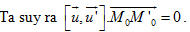
Vậy hai đường thẳng d và d’ cắt nhau. Cách 3 Để tìm tọa độ giao điểm của d và d’, ta giải hệ phương trình sau đây 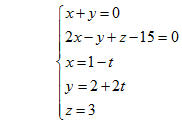
Bằng cách thay các giá trị của x, y, z ở ba phương trình cuối vào hai phương trình đầu của hệ, ta được 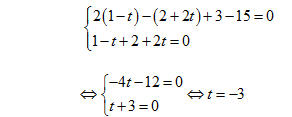
Khi đó x = 4, y = -4, z = 3. Vậy hai đường thẳng d và d’ cắt nhau tại điểm (4; -4; 3). 4. Một số bài toán về tính khoảng cách Ta đã có các công thức để tính khoảng cách giữa hai điểm và khoảng cách từ một điểm tới một mặt phẳng. Bây giờ, ta xét khoảng cách từ một điểm tới một đường thẳng và khoảng cách giữa hai đường thẳng chéo nhau. Bài toán 1. Tính khoảng cách h từ một điểm M đến đường thẳng d đi qua điểm M0 và có vectơ chỉ phương 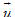 . . Cách giải 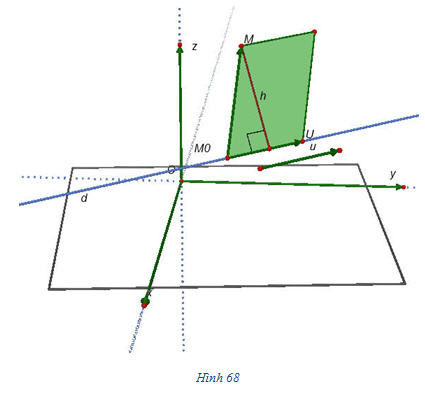
Tải trực tiếp tệp hình học động (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h68.cg3
Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Gọi U là điểm sao cho 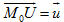 (h.68). (h.68). Nếu M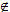 d thì diện tích S của hình bình hành có hai cạnh M0M và M0U là d thì diện tích S của hình bình hành có hai cạnh M0M và M0U là 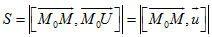
Vì khoảng cách h cần tìm là chiều cao của hình bình hành ứng với cạnh M0U nên ta có 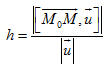
Nếu M d thì hiển nhiên h = 0 và công thức nói trên vẫn đúng. d thì hiển nhiên h = 0 và công thức nói trên vẫn đúng.  3 Tính khoảng cách từ điểm M(4; -3; 2) đến đường thẳng d có phương trình 3 Tính khoảng cách từ điểm M(4; -3; 2) đến đường thẳng d có phương trình

Bài toán 2. Tính khoảng cách h giữa hai đường thẳng chéo nhau d1 và d2, biết d1 đi qua điểm M1 và có vectơ chỉ phương 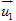 ; d2 đi qua điểm M2 và có vectơ chỉ phương ; d2 đi qua điểm M2 và có vectơ chỉ phương 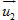 . . Cách giải (h.69) 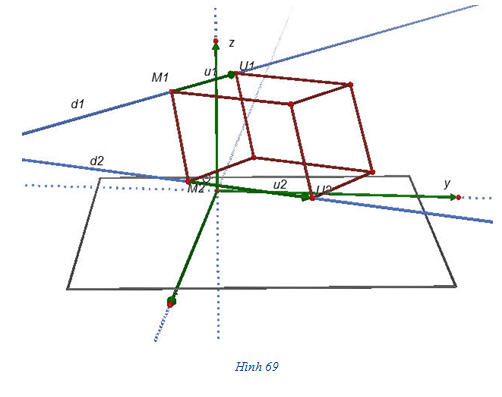
Tải trực tiếp tệp hình học động (Nhấn chuột phải chọn Save Target As hoặc Lưu Liên Kết dưới dạng): L12_ch3_h69.cg3
Xem trực tiếp hình vẽ động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212b_Win.exe ) Lấy các điểm U1 và U2 sao cho 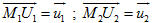 . Xét hình hộp có ba cạnh là M1U1, M2U2, M1M2. Ta biết rằng thể tích V của hình hộp đó là . Xét hình hộp có ba cạnh là M1U1, M2U2, M1M2. Ta biết rằng thể tích V của hình hộp đó là 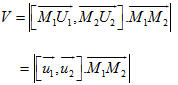
Nếu ta xem M1M2 là cạnh bên của hình hộp đó thì diện tích mặt đáy của hình hộp là 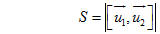
Khi đó, khoảng cách h giữa hai đường thẳng d1 và d2 chính là chiều cao của hình hộp. Vậy ta có: 
 4 Hãy tính khoảng cách giữa hai đường thẳng chéo nhau d1, d2 có phương trình như sau: 4 Hãy tính khoảng cách giữa hai đường thẳng chéo nhau d1, d2 có phương trình như sau:
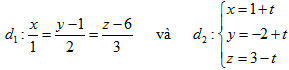
Câu hỏi và bài tập 24. Viết phương trình tham số và chính tắc (nếu có) của các đường thẳng sau đây: a) Các trục tọa độ Ox, Oy, Oz ; b) Các đường thẳng đi qua điểm M0(x0; y0; z0) (với x0.y0.z0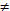 0 ) và song song với mỗi trục tọa độ ; 0 ) và song song với mỗi trục tọa độ ; c) Đường thẳng đi qua M(2; 0; -1) và có vectơ chỉ phương 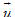 (-1; 3; 5); (-1; 3; 5); d) Đường thẳng đi qua N(-2; 1; 2) và có vectơ chỉ phương 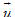 (0; 0; -3); (0; 0; -3); e) Đường thẳng đi qua N(3; 2; 1) và vuông góc với mặt phẳng 2x - 5y + 4 = 0; g) Đường thẳng đi qua hai điểm P(2; 3; -1) và Q(1; 2; 4) . 25. Viết phương trình tham số, chính tắc (nếu có) của các đường thẳng sau đây: a) Đường thẳng đi qua điểm (4; 3; 1) và song song với đường thẳng có phương trình: 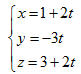
b) Đường thẳng đi qua điểm (-2; 3; 1) và song song với đường thẳng có phương trình: 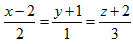
26. Viết phương trình hình chiếu vuông góc của đường thẳng 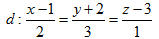
trên mỗi mặt phẳng tọa độ. 27. Cho đường thẳng 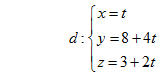 và mặt phẳng (P): x + y + z - 7 = 0. a) Tìm một vectơ chỉ phương của d và một điểm nằm trên d. b) Viết phương trình mặt phẳng đi qua d và vuông góc với mp(P). c) Viết phương trình hình chiếu vuông góc của d trên mp(P). 28. Xác định vị trí tương đối giữa các cặp đường thẳng d và d’ cho bởi phương trình:  d’ là giao tuyến của hai mặt phẳng: d’ là giao tuyến của hai mặt phẳng:
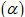 : x + y - z = 0, : x + y - z = 0,
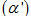 : 2x - y + 2z = 0. : 2x - y + 2z = 0.
29. Viết phương trình đường thẳng đi qua A(1; -1; 1) và cắt cả hai đường thẳng sau đây: 
30. Viết phương trình đường thẳng song song với đường thẳng d1 và cắt cả hai đường thẳng d2 và d3, biết phương trình của d1, d2 và d3 là: 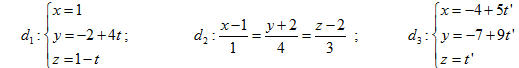
31. Cho hai đường thẳng: 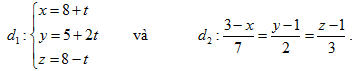
a) Chứng tỏ rằng hai đường thẳng đó chéo nhau. b) Viết phương trình mặt phẳng đi qua gốc tọa độ O, song song với cả d1 và d2. c) Tính khoảng cách giữa hai đường thẳng d1 và d1. d) Viết phương trình đường vuông góc chung của hai đường thẳng đó. 32. Cho đường thẳng d và mặt phẳng 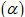 có phương trình: có phương trình: 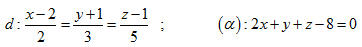
a) Tìm góc giữa d và 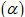 . . b) Tìm tọa độ giao điểm của d và 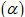 . . c) Viết phương trình hình chiếu vuông góc của d trên 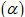 . . 33. Cho đường thẳng 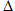 và mp(P) có phương trình: và mp(P) có phương trình: 
a) Xác định tọa độ giao điểm A của 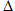 và (P). và (P). b) Viết phương trình đường thẳng đi qu A, nằm trong (P) và vuông góc với 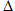 . . 34. a) Tính khoảng cách từ điểm M(2; 3; 1) đến đường thẳng 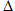 có phương trình: có phương trình: 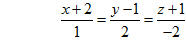
b) Tính khoảng cách từ điểm N(2; 3; -1) đến đường thẳng 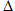 đi qua điểm M0(-0,5; 0; -0,75) và có vectơ chỉ phương đi qua điểm M0(-0,5; 0; -0,75) và có vectơ chỉ phương 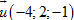 . . 35. Tìm khoảng cách giữa hai đường thẳng sau: 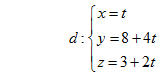
School@net
|

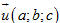 (h.66). Vì
(h.66). Vì 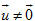 nên ta phải có .
nên ta phải có .
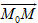 cùng phương với vectơ
cùng phương với vectơ 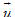 , tức là có số
, tức là có số 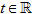 sao cho
sao cho 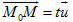 . Chú ý rằng
. Chú ý rằng 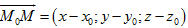 nên điều kiện nói trên tương đương với:
nên điều kiện nói trên tương đương với: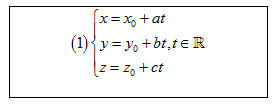
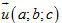 .
. 1 Cho đường thẳng d có phương trình tham số:
1 Cho đường thẳng d có phương trình tham số: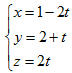

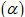 và
và 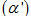 có phương trình:
có phương trình: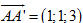 là một vectơ chỉ phương của d, ngoài ra d đi qua điểm A nên d có phương trình tham số là
là một vectơ chỉ phương của d, ngoài ra d đi qua điểm A nên d có phương trình tham số là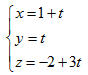
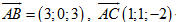 .
.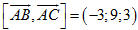 nên một vectơ pháp tuyến của mặt phẳng (ABC) là
nên một vectơ pháp tuyến của mặt phẳng (ABC) là 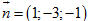 .
.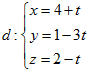
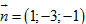 và đi qua A(0 ; 0 ; 2) nên có phương trình là
và đi qua A(0 ; 0 ; 2) nên có phương trình là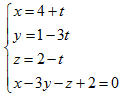
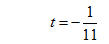
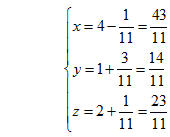
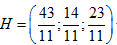
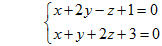
 là vectơ pháp tuyến của mặt phẳng
là vectơ pháp tuyến của mặt phẳng  là vectơ pháp tuyến của mặt phẳng
là vectơ pháp tuyến của mặt phẳng  và
và  nên nó có vectơ chỉ phương là
nên nó có vectơ chỉ phương là  .
.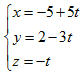
 nên d có phương trình tham số là:
nên d có phương trình tham số là: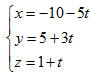
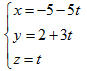

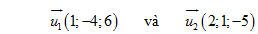
 . Ta tính được
. Ta tính được  và do đó d3 có phương trình chính tắc là
và do đó d3 có phương trình chính tắc là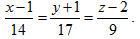
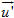 . Dựa vào vectơ
. Dựa vào vectơ 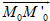 , ta có thể biết được vị trí tương đối giữa hai đường thẳng d và d’.
, ta có thể biết được vị trí tương đối giữa hai đường thẳng d và d’.

 Khi nào hai đường thẳng d và d’ nói trên vuông góc với nhau?
Khi nào hai đường thẳng d và d’ nói trên vuông góc với nhau?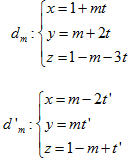
 . Đường thẳng d’m đi qua điểm M’(m; 0; 1 - m) và có vectơ chỉ phương là
. Đường thẳng d’m đi qua điểm M’(m; 0; 1 - m) và có vectơ chỉ phương là  .
. .
.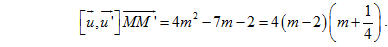
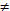 2 và m
2 và m và
và  không cùng phương, suy ra hai đường thẳng đã cho cắt nhau;
không cùng phương, suy ra hai đường thẳng đã cho cắt nhau; và
và  cũng không cùng phương, suy ra hai đường thẳng đã cho cắt nhau.
cũng không cùng phương, suy ra hai đường thẳng đã cho cắt nhau.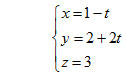
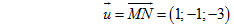
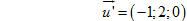
 .
. , tức là ba vectơ
, tức là ba vectơ  đồng phẳng.
đồng phẳng. không cùng phương.
không cùng phương. .
. .
. .
. .
.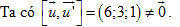
 d, điểm M’0(1; 2; 3)
d, điểm M’0(1; 2; 3) 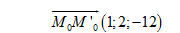
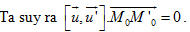
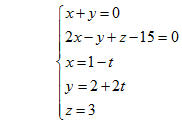
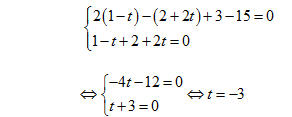

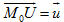 (h.68).
(h.68).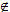 d thì diện tích S của hình bình hành có hai cạnh M0M và M0U là
d thì diện tích S của hình bình hành có hai cạnh M0M và M0U là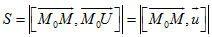
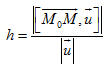
 d thì hiển nhiên h = 0 và công thức nói trên vẫn đúng.
d thì hiển nhiên h = 0 và công thức nói trên vẫn đúng.
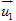 ; d2 đi qua điểm M2 và có vectơ chỉ phương
; d2 đi qua điểm M2 và có vectơ chỉ phương 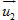 .
.
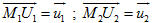 . Xét hình hộp có ba cạnh là M1U1, M2U2, M1M2. Ta biết rằng thể tích V của hình hộp đó là
. Xét hình hộp có ba cạnh là M1U1, M2U2, M1M2. Ta biết rằng thể tích V của hình hộp đó là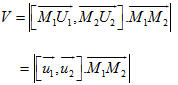
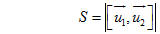

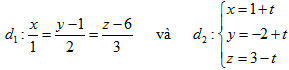
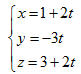
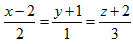
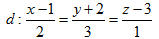
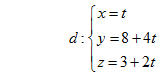
 d’ là giao tuyến của hai mặt phẳng:
d’ là giao tuyến của hai mặt phẳng:
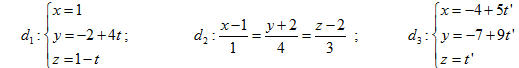
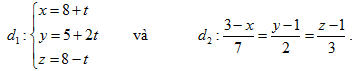
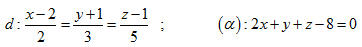
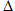 và mp(P) có phương trình:
và mp(P) có phương trình:
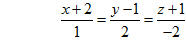
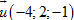 .
.




