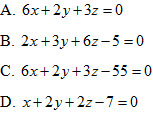+ Điểm M có tọa độ  . . + Nếu điểm A(xA ; yA ; zA) và điểm B = (xB ; yB ; zB) thì 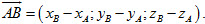
2. Tích vô hướng và tích có hướng. Cho  và và  . . + Tích vô hướng của  và và 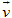 là số: là số:  . . + Tích có hướng của  và và 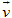 là vectơ là vectơ 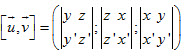 Vectơ  vuông góc với cả vuông góc với cả  và và 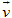 . . + Một số tính chất: 
+ Diện tích hình bình hành:  . . + Thể tích hình hộp: 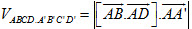 3. Phương trình mặt cầu. Phương trình có dạng 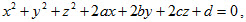
với điều kiện  , là phương trình mặt cầu có tâm , là phương trình mặt cầu có tâm  và có bán kính và có bán kính  . . 4. Phương trình mặt phẳng Mặt phẳng đi qua điểm  với vectơ pháp tuyến với vectơ pháp tuyến  có phương trình: có phương trình: 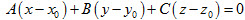
Phương trình 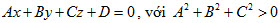
là phương trình của mặt phẳng có vectơpháp tuyến là  . . 5. Phương trình đường thẳng Cho đường thẳng d đi qua điểm  và có vectơ chỉ phương và có vectơ chỉ phương  Khi đó: Khi đó: + Phương trình tham số của dlà + Phương trình chính tắc của d (khi abc ≠ 0) là 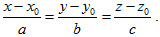
6. Vị trí tương đối giữa hai mặt phẳng Nếu (α) có phương trình Ax + By + Cz + D = 0 và (α’)có phương trình A’x + B’y + C’z + D’ = 0thì + (α) và (α’) cắt nhau khi và chỉ khi A : B : C ≠ A’ : B’ : C’; 
+ (α) và (α’) vuông góc với nhau khi và chỉ khi AA’ + BB’ + CC’ = 0.
7. Vị trí tương đối giữa hai đường thẳng
Nếu đường thẳng d đi qua điểm M0, có vectơ chỉ phương  và đường thẳng d’ đi qua điểm M’0, có vectơ chỉ phương và đường thẳng d’ đi qua điểm M’0, có vectơ chỉ phương  thì: thì: 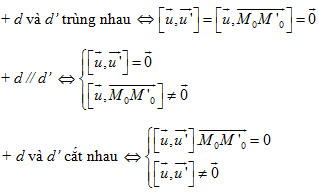
8. Khoảng cách
+ Khoảng cách giữa hai điểm A(xA ; yA ; zA) và B(xB ; yB ; zB) là 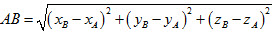
+ Khoảng cách từ điểm  đến mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 là đến mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 là 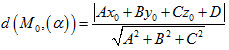
+ Khoảng cách từ điểm M1 đến đường thẳng ∆ đi qua M0 và có vectơ chỉ phương  là là 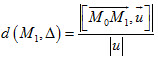
+ Khoảng cách giữa hai đường thẳng chéo nhau ∆ và ∆’, trong đó ∆ đi qua điểm M0 và có vectơ chỉ phương  , còn ∆’ đi qua điểm M’0 và có vectơ chỉ phương , còn ∆’ đi qua điểm M’0 và có vectơ chỉ phương  là là 
II - Câu hỏi tự kiểm tra 1. Cho biết tọa độ của hai điểm A, B, làm thế nào để tìm: a) Tọa độ của vectơ  ; ; b) Khoảng cách giữa hai điểm A và B ; c) Tọa độ của trung điểm đoạn thẳng AB ? 2. Cho tọa độ bốn đỉnh của một hình tứ diện, làm thế nào để tìm: a) Tọa độ của trọng tâm tứ diện; b) Tọa độ của tâm và bán kính mặt cầu ngoại tiếp tứ diện; c) Thể tích tứ diện; d) Độ dài đường cao ứng với một mặt của tứ diện? 3. Bằng phương pháp tọa độ, làm thế nào để chứng minh: a) Hai vectơ cùng phương; b) Ba vectơ đồng phẳng; c) Ba điểm thẳng hàng; d) Bốn điểm không đồng phẳng? 4. Trong mỗi trường hợp sau, hãy nêu cách viết phương trình mặt phẳng: a) Đi qua ba điểm không thẳng hàng; b) Đi qua một điểm và vuông góc với một đường thẳng cho trước; c) Đi qua một điểm và song song với hai đường thẳng chéo nhau cho trước; d) Đi qua một đường thẳng và song song với một đường thẳng cho trước; e) Đi qua một điểm và vuông góc với hai mặt phẳng cho trước; g) Chứa hai đường thẳng song song hoặc cắt nhau; h) Đi qua một đường thẳng và vuông góc với một mặt phẳng cho trước. 5. Trong mỗi trường hợp sau, làm thế nào để viết phương trình đường thẳng: a) Đi qua một điểm và có vectơ chỉ phương cho trước; b) Đi qua hai điểm phân biệt cho trước; c) Đi qua một điểm và vuông góc với một mặt phẳng cho trước; d) Đi qua một điểm và song song với hai mặt phẳng cắt nhau cho trước; e) Đi qua một điểm và cắt hai đường thẳng chéo nhau cho trước; g) Là đường vuông góc chung của hai đường thẳng chéo nhau cho trước ? 6. Bằng phương pháp tọa độ, làm thế nào để xác định vị trí tương đối: a) Giữa hai mặt phẳng; b) Giữa hai đường thẳng ? 7. Bằng phương pháp tọa độ, làm thế nào để tính khoảng cách: a) Từ một điểm đến một mặt phẳng ; b) Từ một điểm đến một đường thẳng ; c) Giữa hai đường thẳng chéo nhau ; d) Giữa hai đường thẳng song song ; e) Giữa hai mặt phẳng song song ; g) Giữa đường thẳng và mặt phẳng song song với đường thẳng đó ? 8. Trong mỗi trường hợp sau, làm thế nào để xác định tọa độ của điểm: a) Là hình chiếu của một điểm trên một mặt phẳng cho trước ; b) Là hình chiếu của một điểm trên một đường thẳng cho trước ; c) Đối xứng với một điểm cho trước qua một mặt phẳng cho trước ? III - Bài tập 1. Cho bốn điểm A(1;6;2),B(4;0;6),C(5;0;4), D(5;1;3). a) Chứng minh rằng bốn điểm đó không đồng phẳng. b) Tính thể tích tứ diện ABCD. c) Viết phương trình mp(BCD). d) Viết phương trình mặt cầu tâm A tiếp xúc với mp(BCD). Tìm tọa độ tiếp điểm. 2. Cho hai điểm A(1 ; -1 ; 2),B(3;1;1) và mặt phẳng (P): x – 2y + 3z – 5 = 0. a) Tìm tọa độ điểm A’ đối xứng với điểm A qua mp(P). b) Tìm góc giữa đường thẳng AB và mp(P). c) Viết phương trình mặt phẳng (Q) đi qua A, B và vuông góc với mp(P). d) Tìm tọa độ giao điểm I của đường thẳng AB và mp(P). Viết phương trình đường thẳng ∆ nằm trong (P), đi qua I và vuông góc với AB. 3. Cho đường thẳng d và mp(P) có phương trình: 
a) Viết phương trình đường thẳng d’ là hình chiếu vuông góc của d trên mp(P). b) Viết phương trình đường thẳng d1 là hình chiếu song song của d trên mp(P) theo phương Oz. c) Viết phương trình đường thẳng đi qua gốc tọa độ O, cắt d và song song với mp(P). 4. Cho điểm A (2;3;1) và hai đường thẳng: 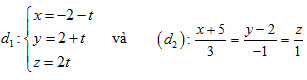
a) Viết phương trình mp(P) đi qua A và d1. b) Viết phương trình mp(Q) đi qua A và d2. c) Viết phương trình đường thẳng d đi qua A, cắt cả d1 và d2. d) Tính khoảng cách từ A đến d2. 5. Cho hai đường thẳng: 
a) Chứng minh hai đường thẳng đó chéo nhau. Tính góc giữa chúng. b) Tính khoảng cách giữa d và d’. c) Viết phương trình đường vuông góc chung của d và d’. d) Viết phương trình đường thẳng song song với Oz, cắt cả d và d’. 6. Cho hai đường thẳng: 
a) Chứng minh rằng d và d’ đồng phẳng. Viết phương trình mặt phẳng (P) chứa chúng. b) Tính thể tích hình tứ diện giới hạn bởi mp(P) và ba mặt phẳng tọa độ. c) Viết phương trình mặt cầu ngoại tiếp tứ diện nói trên. 7. Cho hai đường thẳng: 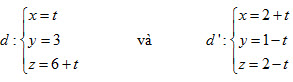
a) Chứng minh rằng d, d’ chéo nhau và vuông góc với nhau. b) Viết phương trình mp(P) đi qua d và vuông góc với d’, phương trình mp(Q) đi qua d’ và vuông góc với d. c) Viết phương trình chính tắc của đường vuông góc chung của d và d’. 8. Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình: (P) : 2x – y + z = 0và (Q) : x + y + 2z – 1 = 0 a) Chứng minh rằng (P) và (Q) cắt nhau. Tìm góc giữa hai mặt phẳng đó. b) Viết phương trình đường thẳng d đi qua A(1;2;-3), song song với cả (P) và (Q). c) Viết phương trình mp(R) đi qua B(-1;3;4), vuông góc với cả (P) và (Q). 9. Cho mặt cầu (S) có phương trình:  . . a) Tìm tọa độ tâm mặt cầu và tính bán kính mặt cầu. b) Tùy theo giá trị của k, hãy xét vị trí tương đối của mặt cầu (S) và mp(P) với (P) : x + y – z + k = 0 c) Mặt cầu cắt ba trục Ox, Oy, Oz lần lượt tại ba điểm A, B, Ckhác với gốc tọa độ O. Viết phương trình mp(ABC). d) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm B. e) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) và song song với mặt phẳng (Q) có phương trình 4x + 3y – 12z – 1 = 0. 10. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Trên các tia AA’, AB, AD (có chung gốc A), lần lượt lấy các điểm M, N, P khác A sao cho AM = m, AN = n và AP = p. a) Tìm sự liên hệ giữa m, n và p sao cho mp(MNP) đi qua đỉnh C’ của hình lập phương. b) Trong trường hợp mp(MNP) luôn đi qua C’, hãy tìm thể tích bé nhất của tứ diện AMNP. Khi đó tứ diện AMNP có tính chất gì? IV - Câu hỏi trắc nghiệm 1. Cho ba điểm M(2;0;0), N(0;-3;0), P(0;0;4). Nếu MNPQ là hình bình hành thì tọa độ của điểm Q là A. (-2;-3;4); B. (3;4;2); C. (2;3;4); D. (-2;-3;-4). 2. Cho ba điểm  . Tam giác ABC là . Tam giác ABC là (A). Tam giác cân đỉnh A; (B). Tam giác vuông đỉnh A; (C). Tam giác đều; (D). Không phải như (A), (B), (C). 3. Cho tam giác ABC có  . Độ dài đường cao của tam giác kẻ từ C là . Độ dài đường cao của tam giác kẻ từ C là 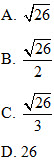
4. Ba đỉnh của một hình bình hành có tọa độ là  . Diện tích của hình bình hành đó bằng . Diện tích của hình bình hành đó bằng
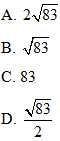
5. Cho  . Thể tích của tứ diện ABCD là . Thể tích của tứ diện ABCD là
A. 1 B. 2 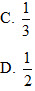
6. Cho  . Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D là . Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D là
A. 3 B. 1 C. 2 
7. Cho bốn điểm  . Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ: . Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ:
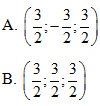
C. (3;3;3)
D. (3;-3;3) 8. Bán kính của mặt cầu tâm I(3;3;-4), tiếp xúc với trục Oy bằng A. 5 B. 4 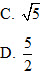
9. Mặt cầu tâm I (2;1;-1), tiếp xúc với mặt phẳng tọa độ (Oyz) có phương trình là
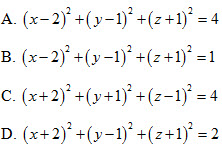
10. Cho ba điểm  . Mặt phẳng (ABC) có phương trình là . Mặt phẳng (ABC) có phương trình là
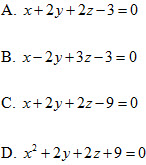
11. Cho ba điểm  . Phương trình nào sau đây không phải là phương trình mặt phẳng (ABC) ? . Phương trình nào sau đây không phải là phương trình mặt phẳng (ABC) ?
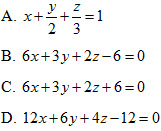
12. Cho hai điểm A(1;3;-4) và B(-1;2;2). Phương trình mặt phẳng trung trực của đoạn AB là
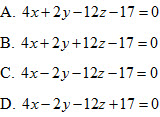
13. Cho  , a, b, clà những số dương thay đổi sao cho , a, b, clà những số dương thay đổi sao cho  . Mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là . Mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
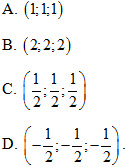
14. Cho điểm A(-1;2;1) và hai mặt phẳng  . .
Mệnh đề nào sau đây là đúng? A. mp(Q) đi qua A và song song với (P); B. mp(Q) không đi qua A và song song với (P); C. mp(Q) đi qua A và không song song với (P); D. mp(Q) không đi qua A và không song song với (P). 15. Cho điểm A . Gọi M, N, P là hình chiếu của A trên ba trục Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là 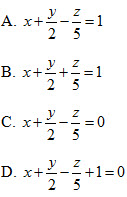
16. Cho mặt cầu (S):  và mặt phẳng và mặt phẳng  . Khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (P) là . Khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (P) là
A. 1 B. 2 C. 3 D. 4 17. Mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C ; trọng tâm tam giác ABClà G(-1;-3;2). Phương trình mặt phẳng (P) là 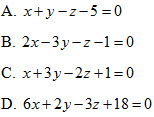
18. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M là trung điểm của cạnh BC. Tính khoảng cách từ A tới mặt phẳng (A’MD).

Hình 70 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch3_h70.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Một học sinh làm như sau: Bước 1. Chọn hệ trục tọa độ như hình 70. Kéo dài DM cắt AB tại E. Khi đó A = (0;0;0) E = (2;0;0) D = (0;1;0) A’ = (0;0;1) Bước 2.Viết phương trình mặt phẳng (A’MD): 
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A. Đúng ; B. Sai ở bước 1 ; C. Sai ở bước 2 ; D. Sai ở bước 3 ; 19. Cho hai điểm  . Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là . Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là 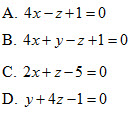
20. Mặt phẳng (P) chứa trục Oz và điểm A(2;-3;5) có phương trình là
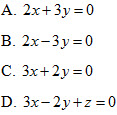
21. Cho mặt phẳng (P)có phương trình  là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa hai mặt phẳng (P) và (Q) bằng là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa hai mặt phẳng (P) và (Q) bằng

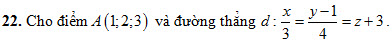
Phương trình mặt phẳng (A ; d)là
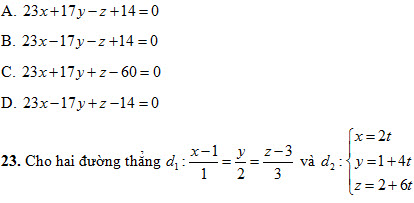
Khẳng định nào sau đây là đúng?
A. d1, d2 cắt nhau B. d1, d2 trùng nhau C. d1 // d2 D. d1, d2 chéo nhau. 24. Cho mặt phẳng 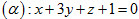 và đường thẳng và đường thẳng 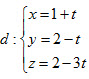 . Tọa độ giao điểm A của d và (α) là . Tọa độ giao điểm A của d và (α) là 
Phương trình nào sau đây cũng là phương trình của đường thẳng d ?
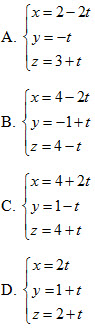
26. Cho hai điểm  và ba phương trình sau: và ba phương trình sau: 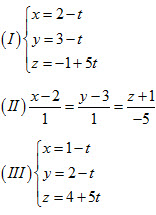
Mệnh đề nào sau đây là đúng?
A. Chỉ có (I) là phương trình của đường thẳng AB; B. Chỉ có (III) là phương trình của đường thẳng AB; C. Chỉ có (I) và (II) là phương trình của đường thẳng AB; D. Cả (I), (II) và (III) đều là phương trình của đường thẳng AB. 27. Cho ba điểm  .Viết phương trình đường thẳng ∆ đi qua trọng tâm G của tam giác ABC và vuông góc với mp(ABC). Một học sinh làm như sau: .Viết phương trình đường thẳng ∆ đi qua trọng tâm G của tam giác ABC và vuông góc với mp(ABC). Một học sinh làm như sau: Bước 1. Tọa độ trọng tâm G của tam giác ABC là 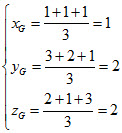
Bước 2. Vectơ pháp tuyến của mp(ABC) là  . .
Bước 3. Phương trình tham số của đường thẳng ∆là 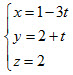
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? A. Đúng; B. Sai ở bước 1; C. Sai ở bước 2; D. Sai ở bước 3. 28. Gọi d là đường thẳng đi qua gốc tọa độ O , vuông góc với trục Ox và vuông góc với đường thẳng 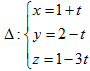 Phương trình của dlà 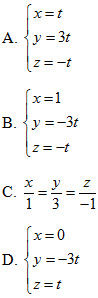
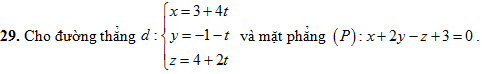
Trong các mệnh đề sau, mệnh đề nào đúng?
A. d song song với (P) ; B. d cắt (P) ; C. d vuông góc với (P) ; D. d nằm trên (P). 30. Cho điểm A(1;1;1) và đường thẳng 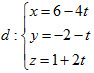 Hình chiếu của A trên d có tọa độ là 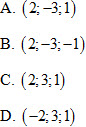
31. Cho tứ diện ABCD có  . Tính khoảng cách giữa hai đường thẳng AC và BD. . Tính khoảng cách giữa hai đường thẳng AC và BD.
Một học sinh làm như sau: 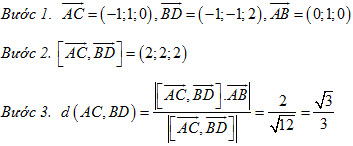
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A. Đúng ; B. Sai ở bước 1 ; C. Sai ở bước 2 ; D. Sai ở bước 3. 
A. 10
B. 5 C. 8 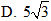
34. Mặt phẳng  cắt các trục tọa độ tại các điểm: cắt các trục tọa độ tại các điểm:
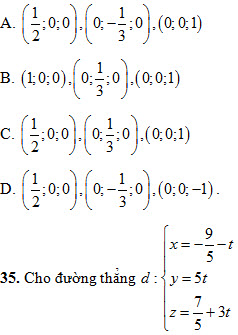
và mặt phẳng  . Gọi d’là hình chiếu của d trên (P). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của d’ ? . Gọi d’là hình chiếu của d trên (P). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của d’ ?
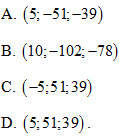
36. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N, Plần lượt là trung điểm của A’B’, BC, DD’. Chứng minh rằng  . .

Hình 71 Tải trực tiếp tệp hình học động ( Nhấn phải chuột vào liên kết rồi chọn Save Target As ): L12_nc_Ch3_h71.cg3 Xem trực tiếp hình học động trên màn hình. ( Nếu không xem được hình ảnh hiển thị xin vui lòng cài đặt Cabri 3D Plugin: Cabri3D_Plugin_212c_Win.exe ) Một học sinh làm như sau: Bước 1. Chọn hệ trục tọa độ như ở hình 71. 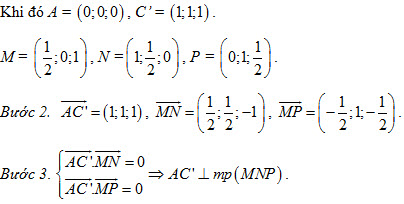
Bài giải trên đúng hay sai ? Nếu sai thì sai ở bước nào ?
A. Đúng ; B. Sai ở bước 1 ; C. Sai ở bước 2 ; D. Sai ở bước 3. 37. Cho đường thẳng 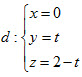
Phương trình đường vuông góc chung của d và trục Ox là
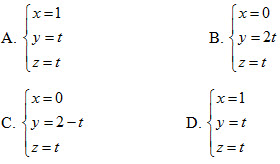
38. Cho mặt phẳng  và điểm M (1;-1;1). Tọa độ của điểm M’ đối xứng với M qua mp(P) là và điểm M (1;-1;1). Tọa độ của điểm M’ đối xứng với M qua mp(P) là
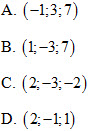
39. Cho điểm A(0;-1;3) và đường thẳng 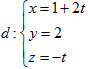
Khoảng cách từ A đến d bằng 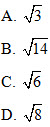
40. Cho điểm M(-1;2;-3). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua các mặt phẳng (Oxy), (Oxz), (Oyz). Phương trình mp(M1M2M3) là
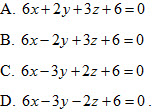
41. Cho mặt cầu  . Phương trình sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ? . Phương trình sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?
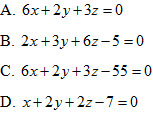
42. Cho mặt cầu  . Trong ba điểm (0;0;0), (1;2;3), (2;-1;-1), có bao nhiêu điểm nằm trong mặt cầu (S) ? . Trong ba điểm (0;0;0), (1;2;3), (2;-1;-1), có bao nhiêu điểm nằm trong mặt cầu (S) ?
A. 0 B. 1 C. 2 D. 3.
School@net
|

 .
.
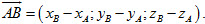


 và
và 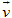 là số:
là số: 
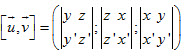



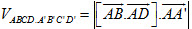
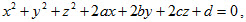
 , là phương trình mặt cầu có tâm
, là phương trình mặt cầu có tâm 
 .
.

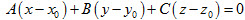
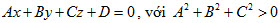



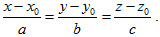

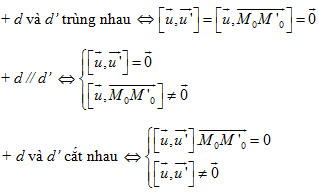
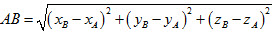
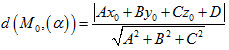
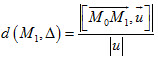
 là
là
 ;
;
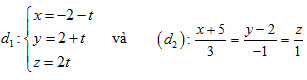


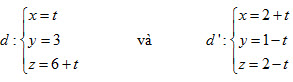
 .
. . Tam giác ABC là
. Tam giác ABC là . Độ dài đường cao của tam giác kẻ từ C là
. Độ dài đường cao của tam giác kẻ từ C là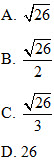
 . Diện tích của hình bình hành đó bằng
. Diện tích của hình bình hành đó bằng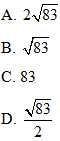
 . Thể tích của tứ diện ABCD là
. Thể tích của tứ diện ABCD là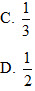
 . Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D là
. Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D là
 . Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ:
. Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ: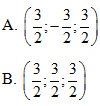
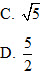
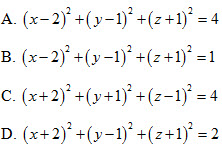
 . Mặt phẳng (ABC) có phương trình là
. Mặt phẳng (ABC) có phương trình là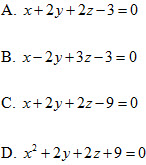
 . Phương trình nào sau đây không phải là phương trình mặt phẳng (ABC) ?
. Phương trình nào sau đây không phải là phương trình mặt phẳng (ABC) ?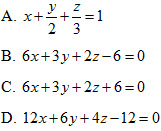
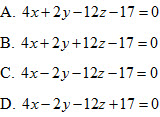
 , a, b, clà những số dương thay đổi sao cho
, a, b, clà những số dương thay đổi sao cho 
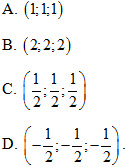
 .
. 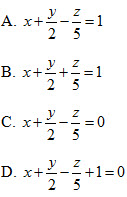

 . Khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (P) là
. Khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (P) là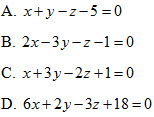


 . Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là
. Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là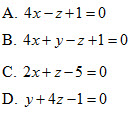
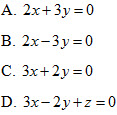
 là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa hai mặt phẳng (P) và (Q) bằng
là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa hai mặt phẳng (P) và (Q) bằng
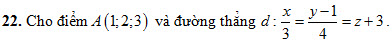
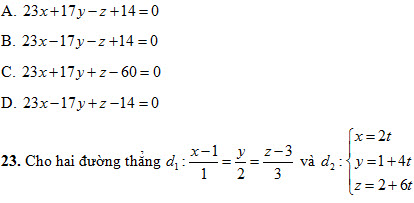
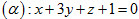
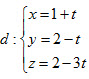

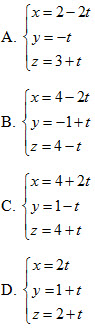
 và ba phương trình sau:
và ba phương trình sau: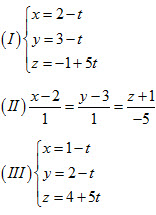

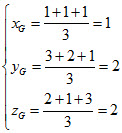

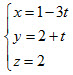
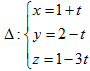
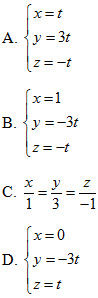
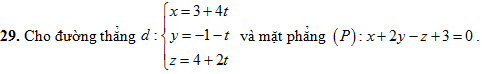
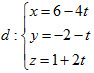
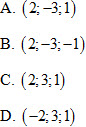

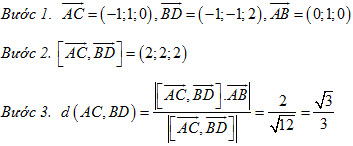

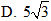
 cắt các trục tọa độ tại các điểm:
cắt các trục tọa độ tại các điểm: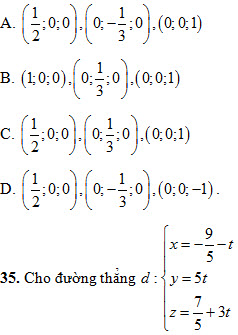

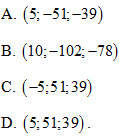
 .
.
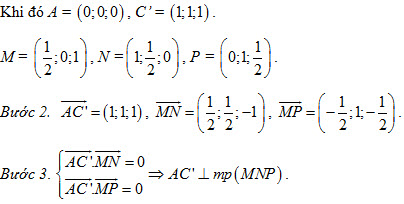
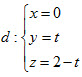
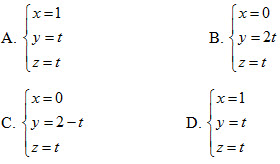

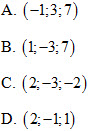
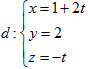
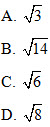
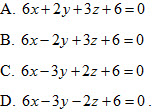
 . Phương trình sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?
. Phương trình sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?