Lịch sử

Ngược dòng lịch sử, vào năm 1952, Andrey Kolmogorov đề xuất rằng thuật toán nhân tay là tối ưu, và bất cứ một thuật toán khác đều cần đến Ω(n2) phép toán cơ bản. Đến năm 1960, Kolmogorov tổ chức một hội thảo ở Moscow và trình bày một loạt các bài toán về độ phức tạp của thuật toán, trong đó có giả thuyết Ω(n2). Trong vòng 1 tuần, Anatolii Alexeevitch Karatsuba, một sinh viên 23 tuổi đã tìm ra một thuật toán chia để trị giải quyết bài toán nhân 2 số n-chữ số chỉ cần O(n(log3)) phép toán cơ bản. Thuật toán này sau đó đã được công bố vào năm 1962, trong khi tác giả của nó cũng không hề biết đến bài báo này.

Thuật toán

Xét phép tính (ax+b)(cx+d)=acx2+(ad+bc)x+bd. Thay vì 1 phép nhân 2 số lớn, chúng ta đã thay thế nó bằng 4 phép nhân 2 số nhỏ hơn. Vậy nếu hai số ban đầu là A và B có 2N chữ số, chúng ta sẽ chọn x=10k, thế thì a, b, c, d đều chỉ có N chữ số. Nhân hai số A và B cần (2N)2=4N2 phép toán, nhân mỗi cặp số nhỏ hơn cần N2 phép toán, như vậy thì nhanh hơn ở chỗ nào? Liệu có cách nào giảm số phép nhân đi nữa không?
Xét tiếp (a+b)(c+d)=ac+ad+bc+bd. Vậy thì chỉ cần tính ac, bd, (a+b)(c+d) là ta đã có đủ 3 hệ số. Khi đó, độ phức tạp sẽ là T(N)=3*T(N/2)+O(N), nghĩa là O(N(log3)), xấp xỉ O(N1.58), quá là hiệu quả.

Các bước thực hiện

1. Nhập hai số X và Y gồm N chữ số
2. Tìm A, B, C, D sao cho X=A*10M+B; Y=C*10M+D với M=N/2
3. Tính A1=A*C; A3=B*D; A2=(A+B)*(C+D)-A1-A3;
4. Kết quả X*Y=A1*10(2M)+A2*10M+A3
Ví dụ: nhân 2 số 1234 và 5678, gồm 4 chữ số M=2; 1234=12*102+34; 5678=56*102+78; A=12, B=34, C=56, D=78.
A1=12*56=672; A3=34*78=2652; A2= (12+34) (56+78)-A1-A3=46*134-672-2652=2840.
1234*5678=672*104+2840*102+2652=7006652
Ở bước 1, khi ta lưu X và Y dưới dạng BigNum thì ở bước 2, tìm 4 số A, B, C, D sẽ vô cùng đơn giản, vì A và C chỉ là lấy từ chữ số đầu đến chữ số thứ M của X và Y, phần còn lại là B và D, bước 3 khi thực hiện phép nhân, ta sẽ dùng đệ quy, áp dụng lại thuật toán Karatsuba cho đến khi A, B, C, D còn ít hơn 121 chữ số thì nhân tay. Lí do sử dụng nhân tay cho số có ít hơn 121 chữ số là vì khi đó, số phép cộng trừ và dời chỗ sẽ làm cho thuật toán Karatsuba chạy kém hiệu quả hơn.

Cài đặt

#include
#include
#include
#define MAX_DIGITS 60000
#define LIMIT 121
void
normalMult(long *a, long *b, long *ret, long d) {
long i, j;
for(i = 0; i < 2 * d; i++) ret[i] = 0;
for(i = 0; i < d; i++) {
for(j = 0; j < d; j++) ret[i + j] += a[i] * b[j];
}
}
void
karatsubaMult(long *a, long *b, long *ret, long d) {
long i;
long *ar = &a[0];
long *al = &a[d/2];
long *br = &b[0];
long *bl = &b[d/2];
long *asum = &ret[d * 5];
long *bsum = &ret[d * 5 + d/2];
long *x1 = &ret[d * 0];
long *x2 = &ret[d * 1];
long *x3 = &ret[d * 2];

// khi d nhỏ thì nhân tay
if(d <= LIMIT) {
normalMult(a, b, ret, d);
return;
}
// tính tổng a+b và c+d
for(i = 0; i < d / 2; i++) {
asum[i] = al[i] + ar[i];
bsum[i] = bl[i] + br[i];
}

// tính 3 hệ số lưu vào cùng 1 mảng
karatsubaMult(ar, br, x1, d/2);
karatsubaMult(al, bl, x2, d/2);
karatsubaMult(asum, bsum, x3, d/2);

// kết hợp lại cho ra kết quả
for(i = 0; i < d; i++) x3[i] = x3[i] - x1[i] - x2[i];
for(i = 0; i < d; i++) ret[i + d/2] += x3[i];
}
void
doCarry(long *a, long d) {
long c;
long i;

c = 0;
for(i = 0; i < d; i++) {
a[i] += c;
if(a[i] < 0) {
c = -(-(a[i] + 1) / 10 + 1);
} else {
c = a[i] / 10;
}
a[i] -= c * 10;
}
}
void Input(long *a, long *d_a) {
char c;
long i;

*d_a = 0;
c = '0';
while(!(c == ' ' || c == EOF)) {
scanf("%c",&c);
a[*d_a] = c - '0';
++(*d_a);
}
// đảo lại mảng lưu số
for(i = 0; i * 2 < *d_a - 1; i++) {
c = a[i], a[i] = a[*d_a - i - 1], a[*d_a - i - 1] = c;
}
}
void Output(long *a, long d) {
long i;
for(i = d - 1; i > 0; i--) if(a[i] != 0) break;
for(; i >= 0; i--) printf("%d", a[i]);
}
int main() {
long a[MAX_DIGITS];
long b[MAX_DIGITS];
long r[6 * MAX_DIGITS];
// chỉ dùng 1 mảng lớn lưu kết quả cùng các giá trị tạm
// | ar*br | al*bl | asum*bsum | giá trị tạm | asum | bsum |
// d d d 3d d/2 d/2
long d_a;
long d_b;
long d;
long i;
clock_t start;
clock_t stop;
Input(a, &d_a);
Input(b, &d_b);

if(d_a < 0 || d_b < 0) {
printf("0 ");
exit(0);
return 0;
}
// cho tất cả các số còn lại của a và b là 0
i = (d_a > d_b) ? d_a : d_b;
for(d = 1; d < i; d *= 2);
for(i = d_a; i < d; i++) a[i] = 0;
for(i = d_b; i < d; i++) b[i] = 0;

//nhân dùng thuật toán karatsuba

start = clock(); // dùng để tính thời gian
karatsubaMult(a, b, r, d);
doCarry(r, 2 * d);
start = clock() - start;
Output(r, 2 * d);
printf(" %f ms ", 1000 * (double) start / CLOCKS_PER_SEC);

//nhân tay

start = clock();
normalMult(a, b, r, d);
doCarry(r, 2 * d);
start = clock() - start;
Output(r, 2 * d);
printf(" %f ms ", 1000 * (double) start / CLOCKS_PER_SEC);
}

Kết quả
Trên máy tính xách tay chạy CPU AMD X2 QL-62 2.0 Ghz, bộ nhớ RAM 4 GB, đoạn code trên chạy trong Dev-C++ 4.9.9.2 được kết quả như sau: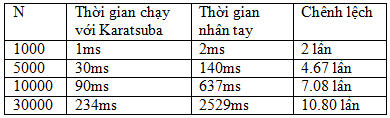

Vậy thì với N tăng lên 30 lần, thuật toán Karatsuba đã vượt hoàn toàn cách nhân tay thông thường tới 10 lần, nhân 2 số có 30000 chữ số chỉ mất chưa đầy 0.3s, trong khi cách cài đặt này hoàn toàn chưa tối ưu.

Hướng tối ưu

Bạn đọc có thể tìm cách tối ưu cách cài đặt hơn nữa bằng cách đưa về hệ cơ số 2, để có thể sử dụng phép SHL và SHR nhanh hơn. Để tăng được giới hạn tính toán, chúng ta có thể dùng các mảng phụ để lưu biến tạm thay vì lưu chung vào một mảng chính.

Mở rộng

Thay vì chia 2 số ban đầu thành 2 phần, ta có thể chia nó làm 3 phần để được thuật toán Toom-3 với độ phức tạp O(n1.465), thậm chí làm k phần để được thuật toán Toom-k với độ phức tạp O(ne), với e = log(2k − 1) / log(k). Thế nhưng hằng số c của thuật toán Toom-k lại tăng nhanh một cách khủng khiếp, cộng với việc nhân chia cộng trừ để tìm ra kết quả quá rắc rối nên chúng ta không cần thiết phải dùng đến, trừ khi với những phép nhân khá lớn. Tuy nhiên một thuật toán còn nhanh hơn nữa đã ra đời vào năm 1971 mang tên Schönhage–Strassen. Độ phức tạp của thuật toán này chỉ còn là O(NlogN), nhưng chỉ vượt mặt thuật toán Karatsuba khi 2 số ban đầu có nhiều hơn 40000 chữ số. Cài đặt thuật toán này đòi hỏi phải biết về Fast Fourier transforms (FFT)–biến đổi Fourier nhanh nên không khả thi với trình độ học sinh. Vào năm 2007, một thuật toán nữa còn nhanh hơn Schönhage-Strassen được tìm ra, đó là thuật toán Fürer với độ phức tạp nhỏ hơn một chút và chỉ thực sự nhanh khi nhân 2 số vô cùng lớn.

Mặc dù đã hết sức thận trọng và xem xét kỹ lưỡng các ví dụ đưa ra trong bài viết, tuy vậy vẫn có thể không tránh khỏi các sai sót, rất mong nhận được sự đóng góp ý kiến của các bạn độc giả. Mọi góp ý, thắc mắc xin gửi về địa chỉ email: nkvuong@gmail.com.

Schoolnet