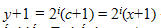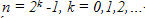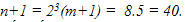Tình huống A được gọi là kết quả, các tình huống Bi được gọi là nguyên nhân.
Như vậy, lập luận theo phương pháp nhân – quả chẳng qua là xác định những nguyên nhân nào dẫn đến kết quả trung gian hiện có.
Sau khi xác định được các tình huống Bi chúng ta lại lại chọn ra một số tình huống liên quan đến lời giải và lần lượt khảo sát chúng theo cách lập luận trên: Những tình huống nào có thể dẫn đến tình huống Bi?
Thực ra phương pháp này đã khá quen thuộc đối với các bạn học sinh phổ thông với tên gọi là lần ngược hoặc suy luận từ dưới lên. Tuy nhiên, đôi lúc chúng ta hay quan niệm quá đơn giản là phương pháp lần ngược đòi hỏi phải bắt đầu xuất phát từ kết luận rồi lập luận ngược theo từng bước đến giả thiết.
Để vận dụng sáng tạo phương pháp nhân-quả chúng ta có thể bắt đầu với một tình huống ban đầu nào đó, không nhất thiết là kết luận, miễn là có lợi cho quá trình giải là được.
Lập luận nhân – quả thường được vận dụng cho các thuật toán trò chơi.
Bài toán Rectangle Game (Trò chơi chữ nhật, Tài liệu luyện tập IOI 05', Ba Lan)
Cho tờ giấy hình chữ nhật (HCN) chia thành m n ô vuông đơn vị. Hai người chơi là A và B. A luôn đi trước. Một nước đi được mô tả như sau: dùng kéo cắt đôi hình theo một đường kẻ sau đó giao nửa to (có diện tích tính bằng số ô đơn vị) cho người kia. Nếu hai mảnh có diện tích bằng nhau thì giao một mảnh nào đó cho người kia. Người chơi nào đến lượt mình không thể chia được hình, tức là gặp hình chữ nhật kích thước 1x1 chỉ gồm 1 ô đơn vị thì thua. Hãy cho biết A thắng (viết 1) hay thua (viết 0). Giả sử rằng hai đấu thủ đều chơi rất giỏi, tức là có khả năng tính trước được mọi nước đi.
Hình 1 minh họa một ván chơi với hình chữ nhật ban đầu kích thước 5x5. Đầu tiên A cắt dọc và bỏ đi mảnh xám 5x2, giao mảnh trắng 5x3 cho B. Đến lượt mình B cắt ngang rồi bỏ đi mảnh xám 2x3, giao mảnh trắng 3x3 cho A. Tiếp theo, A cũng cắt ngang để bỏ đi mảnh xám 1x3, giao mảnh trắng 2x3 cho B. Tại nước đi thứ tư, B cắt dọc, bỏ đi mảnh xám 2x1, giao mảnh trắng 2x2 cho A. Đến bước thứ 5, với hình 2x2, A chỉ còn một cách duy nhất là chia đôi hình thành hai mảnh 1x2 bằng nhau rồi giao một mảnh 1x2 cho B. Cuối cùng B chia đôi mảnh này thành hai hình đơn vị 1x1 và giao một hình cho A. A thua vì đã hết cách đi.
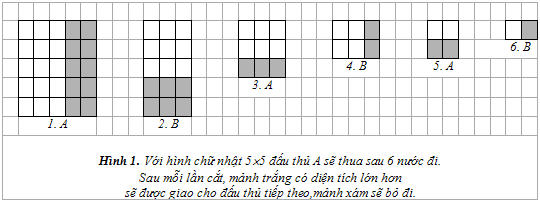
Sau mỗi lần cắt, mảnh trắng có diện tích lớn hơn sẽ được giao cho đấu thủ tiếp theo,mảnh xám sẽ bỏ đi.
Các trò chơi loại này có chung những đặc điểm như sau:
(1) Hữu hạn: sau một số nước đi trò chơi kết thúc,
(2) Chỉ có thắng hoặc thua, không có thế hòa.
Để tính toán cách đi ta tuân thủ theo nguyên tắc: Xác định một thế T thỏa hai tính chất sau:
(i) Với mọi cách đi thế T sẽ được chuyển thành thế V # T.
(ii) Tồn tại một cách đi để chuyển thế V thành thế T.
Thế T được gọi là bất biến của trò chơi. Bạn cần lưu ý đến hai thuật ngữ "với mọi" và "tồn tại" trong phát biểu trên.
Việc xác định hướng giải của thuật toán theo nguyên tắc như trên thường được gọi là heurstics (gốc từ Hylạp, đọc là ơ-ris-tic có nghĩa là kinh nghiệm, định hướng).
Bạn dễ dàng nhận ra bất biến đơn giản đầu tiên của trò chơi này là: hình được cho là hình vuông. Thật vậy, nếu nhận được hình vuông mxm thì với mọi cách cắt A đều chia hình vuông đó thành hai hình chữ nhật dxm và cxm, với d+c=m. A buộc phải giao mảnh có diện tích lớn hơn cho B. Giả sử d x(m div 2). Khi đó c x d và B sẽ nhận được mảnh trắng kích thước cxm >= dxm. B sẽ cắt d ô trên cạnh m để chia mảnh này thành hai hình, hình vuông kích thước cxc và hình chữ nhật kích thước cxd. Ta thấy, vì d <= c nên cxd<= cxc, nghĩa là B sẽ giao cho A mảnh hình vuông cxc. Tóm lại, bất biến ta tìm được trong trường hợp này là
T: mảnh hình vuông. Ta thấy,
• Với mọi cách cắt (T: mảnh vuông) sẽ được chuyển thành (V: mảnh chữ nhật).
• Với mảnh chữ nhật V, tồn tại một cách cắt để chuyển mảnh hình vuông cho đối phương.

Cách đi của B khi A gặp thế thua là hình vuông
Nếu A cắt d ô tại một cạnh thì B cắt d ô tại cạnh còn lại
Bất biến T: mảnh hình vuông dẫn đến thua nên ta gọi vắn tắt T là thế thua, hoặc bất biến thua theo nghĩa ai gặp phải thế đó sẽ thua. Từ thế thua này ta cố gắng tổng quát hóa để tìm các thế thua khác.
Ta thử xét hai nước đi liên tiếp AB.
Giả sử đến một lúc nào đó A gặp một thế chắc thua T. A chọn một nước đi, sau đó giao mảnh lớn cho B. Lưu ý rằng, do A giữ thế thua nên với nước đi này A chỉ có thể giao cho B hình đảm bảo thế thắng V. Do B chơi giỏi nên tại nước đi thứ 2, B sẽ tìm được nước đi để chuyển V thành T và giao cho A hình chữ nhật F dẫn đến thế thua T. Gọi kích thước của hình chữ nhật F này là mxn. Thử hỏi trước khi B chia thì hình này có thể có kích thước là bao nhiêu và trước đó một bước nữa thì hình A cầm trong tay lúc đầu có kích thước là bao nhiêu?
Để trả lời câu hỏi trên ta thử tìm trong "thùng rác" những mảnh G mà B có thể bỏ đi rồi ghép vào với F. Khi đó ta sẽ được hình FG chính là hình mà B có trong tay trước khi chia. Gọi kích thước của hình G này là xxy, ta thấy, theo điều kiện của đầu bài, hình G phải có diện tích nhỏ hơn hình F và G phải có một cạnh bằng với một cạnh của F. Ký hiệu S(H) là diện tích của hình chữ nhật H. Nhận xét trên dẫn đến hai trường hợp sau:
Trường hợp thứ nhất: x=m. Khi đó, S(G) = mxy <= S(F) = mxn, từ đây suy ra 1 <= y <= n, tức là y sẽ có thể nhận các giá trị từ 1 đến n và trước đó y phải nhận giá trị n+1 (bạn hãy tự lý giải vì sao?) tức là hình chữ nhật FG mà A cầm trong tay lúc đầu phải có kích thước mx(2n+1).
Trường hợp thứ hai: y=n. Lập luận tương tự như trường hợp thứ nhất ta thu được 1 <= x<= m và hình chữ nhật A cầm trong tay lúc đầu phải có kích thước (2m+1)xn.
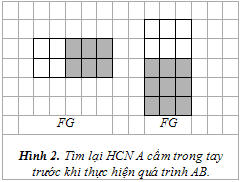
trước khi thực hiện quá trình AB.
Tóm lại, nếu thế thua là HCN mxn thì các thế thua khác chỉ có thể là HCN (2m+1)xn hoặc mx(2n+1).
Để lập công thức tổng quát thể hiện tương quan giữa m và n đối với các thế thua ta tạm thời cố định cạnh m và để ý rằng mọi hình vuông mxm đều là thế thua. Gọi dãy giá trị biến thiên của n là n1, n2,…,ni,…, ta có
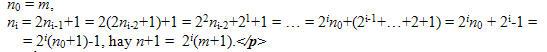
Vậy nếu A nhận được HCN kích thước mn với tương quan giữa các cạnh là

thì A sẽ thua.
Muốn hoàn tất công thức (1) ta còn phải chứng minh thêm một vài chi tiết nữa.
Cụ thể là ta phải chứng minh rằng với HCN mn thỏa tương quan (1) và A đi trước thì dù A cắt dọc hay cắt ngang hình này B đều có cách cắt để tạo ra hai HCN, trong đó HCN có diện tích lớn hơn sẽ thỏa bất biến (1). Trường hợp i=0 cho ta hình vuông với n=m ta đã xét, do đó ta chỉ xét với các trường hợp i >=1. Thật vậy, ta gọi m là chiều rộng và n là chiều dài của HCN có trong tay A và xét hai khả năng cắt hình của A.
Trường hợp thứ nhất: A cắt dọc d ô từ cạnh n để tạo ra hai hình mxd và mxc, với c+d=n và d <= c, tức là HCN mxc có diện tích lớn hơn và được trao cho B. Nhận được hình này, B sẽ tiếp tục cắt x ô trên cạnh n để tạo ra hai HCN kích thước mxy và mxx, x+y = c, x < y và giao HCN có diện tích lớn hơn là my cho A. Ta xác định giá trị x để hình my mà A nhận phải thỏa hệ thức (1). Ta thấy, sau các lần cắt của A và B thì chiều dài còn lại của cạnh n sẽ là y = n-(d+x). Ta có
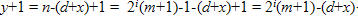
Nếu B chọn x sao cho d+x = 2i-1(m+1) thì
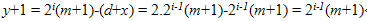
Đây chính là hệ thức (1) cho HCN mxy với i-1 >= 0.
Ta còn phải chứng minh x x 1, nghĩa là B phải thật sự cắt (giải rộng ít nhất 1 ô). Thật vậy, hệ thức (1) cho thấy n là số lẻ, do d và x là các số nguyên dương và d+x=2i-1(m+1), theo điều kiện cắt, ta có
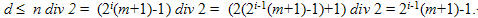
Từ đây suy ra 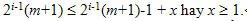
Trường hợp thứ hai: A cắt ngang d ô từ cạnh m để tạo ra hai hình dxn và cxn, với c+d=m và d x c, tức là HCN cxn có diện tích lớn hơn và được trao cho B. Khi đó,  . Từ đây suy ra B sẽ cắt dọc 2id ô từ cạnh n để tạo ra hai hình cx(n-2id) và cx2id. Từ hệ thức n+1 = 2i(c+1)+2id và i > 0 ta suy ra n-2id = 2i(c+1)-1>2ic, tức là hình cx(n-2id) có diện tích lớn hơn hình c2ic và được giao cho A. Hình này có hai cạnh x = c và y = n-2id = 2i(c+1)-1. Tương quan giữa x và y thỏa hệ thức (1), vì . Từ đây suy ra B sẽ cắt dọc 2id ô từ cạnh n để tạo ra hai hình cx(n-2id) và cx2id. Từ hệ thức n+1 = 2i(c+1)+2id và i > 0 ta suy ra n-2id = 2i(c+1)-1>2ic, tức là hình cx(n-2id) có diện tích lớn hơn hình c2ic và được giao cho A. Hình này có hai cạnh x = c và y = n-2id = 2i(c+1)-1. Tương quan giữa x và y thỏa hệ thức (1), vì
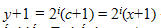
Như vậy A sẽ lại nhận được bất biến T: thế thua.
Dưới đây là bảng tổng kết chiến lược của B trong trường hợp A gặp thế thua.Chú ý rằng bảng này bao hàm cả trường hợp hình vuông. Ta luôn giả thiết n x m.

Cách đi của B khi A gặp thế thua thỏa hệ thức (1)
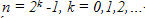
1. Nếu i=0 và A cắt d ô tại một cạnh thì B cắt d ô tại cạnh còn lại.
2. Nếu i > 0 và A cắt d ô tại cạnh dài n thì B cắt tiếp2i-1(m+1)-d ô tại chính cạnh đó.
3. Nếu i > 0 và A cắt d ô tại cạnh ngắn m thì B cắt 2id ô tại cạnh dài n.
Hàm RGame(m,n) dưới đây nhận giá trị vào là chiều rộng m và chiều dài n của HCN và cho giá trị 1 nếu A thắng, giá trị 0 nếu A thua với giả thiết A là người đi trước. Hàm chỉ đơn giản kiểm tra hệ thức (1) đối với m và n. Để ý rằng toán tử (m shl 1) sẽ dịch số nguyên m qua trái 1 bít nên tương đương với phép toán 2*m.
function RGame(m,n: longint): integer;
var t: longint;
begin
if m > n then
begin
t := m;
m := n;
n := t;
end;
{ n x m }
m := m+1;
n := n+1;
while m < n do m := m shl 1; { m:=2*m }
if (m = n) then rgame := 0
else rgame := 1;
end;
Dựa vào hàm trên ta có thể xây dựng thuật toán xác định nước đi cho một người chơi bất kỳ (A hay B) như sau:
Trước hết kiểm tra xem ta đang ở thế nào, thắng V (rgame=1) hay thua T (rgame=0).
1. Nếu ở thế thắng tức là m và n không thỏa hệ thức (1) thì ta chỉnh lại m hoặc n cho thỏa hệ thức (1) như trong bảng chiến lược trên.
2. Nếu biết rằng mình đang ở thế thua T, hãy tìm cách kéo dài cuộc chơi, thí dụ cắt với d=1 trên cạnh nào dài hơn.
Game 3D
Cắt HCN là trò chơi trong không gian 2 chiều. Bạn dễ dàng tổng qúat hóa trò chơi trên cho không gian 3 chiều, cụ thể là:
Cho hình hộp chữ nhật (HH) với ba kích thước m, n và h. Hai người chơi A và B, A luôn đi trước. Mỗi lượt đi phải cắt hình dọc theo một đường kẻ để chia HH thành hai HH rồi trao HH có thể tích lớn hơn cho đối phương. Ai không chia nổi hình tức là gặp khối lập phương đơn vị 1x1x1 thì thua.
Game 1D
Ta tiếp tục cho trừơng hợp không gian 1 chiều với nội dung như sau:
Cho đoạn thẳng gồm n đơn vị dài. Hai người chơi A và B, A luôn đi trước. Mỗi lượt đi phải chọn một điểm nguyên trong đoạn để chia thành hai đoạn rồi giao đoạn có chiều dài lớn hơn cho đối phương. Ai không chia nổi, tức là gặp đoạn thẳng đơn vị thì thua.
Bài tập
1. Chứng minh rằng bất biến thua cho Game 1D là:
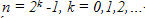
Các số lũy thừa cơ số hai khuyết như trên được gọi là số Mecxen để kỷ niệm nhà toán học đầu tiên nghiên cứu các số đó (nếu 2k -1 là số nguyên tố thì được gọi là số nguyên tố Mecxen).
2. Chứng minh rằng hệ thức (1) luôn luôn thỏa với hai số Mecxen m và n bất kỳ, n x m.
Chú ý rằng điều ngược lại là không đúng, hai số m = 4 và n = 39 không phải là các số Mecxen nhưng chúng thỏa hệ thức (1), vì 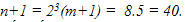
3. Xác định tính đúng của phát biểu sau: Bất biến thua của bài toán 2D là: m=n hoặc m và n đồng thời là các số Mecxen. (Đáp án: chưa đủ tổng quát. Xem lại bài tập 2).
4. Bạn thử nghĩ xem, trong trò chơi 3D các trường hợp sau đây có phải là thế thua không? (không đòi hỏi tổng quát )
a) Ba kích thước bằng nhau, tức là khối lập phương, m = n = h?
b) Hai kích thước bằng nhau, kích thước thứ ba là số Mecxen?
Tiếp tục tổng quát hóa
Liệu có thể phát biểu bài toán cho không gian n chiều tổng quát? Phát biểu thì dễ. Khảo sát kỹ các phương án 1D, 2D và 3D ta thấy rằng, vì các trục của không gian là độc lập với nhau và mỗi lần chỉ được phép cắt trên một cạnh của hình nên bài toán tổng quát sẽ là:
Cho n đoạn thẳng gồm d1, d2,…,dn đơn vị dài. Hai người chơi A và B, A luôn đi trước. Mỗi lượt đi chỉ được chọn một đoạn thẳng và cắt theo một điểm nguyên nằm trong đoạn đã chọn để chia thành hai đoạn con rồi giao đoạn có chiều dài lớn hơn cho đối phương. Ai không chia nổi, tức là gặp thế toàn đoạn thẳng đơn vị thì thua.
Trò chơi bốc sỏi
Có nhiều trò chơi bốc sỏi, bài toán cắt hình tổng quát trong không gian n chiều hóa ra hoàn toàn tương đương với bài toán sau đây:
Cho n đống sỏi gồm d1, d2,…,dn viên mỗi đống. Hai người chơi A và B, A luôn đi trước. Mỗi lượt đi chỉ được chọn một đống và bốc bỏ đi ít nhất là 1 viên, nhiều nhất là một nửa số viên trong đống đã chọn. Ai không còn khả năng bốc, tức là khi mọi đống chỉ còn duy nhất một viên sỏi thì thua .
Ta đã biết, nếu chỉ có một đống thì các thế thua là: số sỏi trong đống là số Mecxen.
Nếu có hai đống với m và n viên sỏi thì thế thua là: m, n thỏa hệ thức (1).
Chúc các bạn một năm mới Vui tươi, Khỏe mạnh và Học giỏi trên mức có thể giải được trọn vẹn bài toán trên.
Nguyễn Xuân Huy
|

 Xuân này xin giới thiệu với các bạn một phương pháp tư duy rất "cổ kính" nhưng tỏ ra có hiệu lực trong khá nhiều trường hợp, đó là tư duy, hay lập luận theo phương pháp nhân – quả.
Xuân này xin giới thiệu với các bạn một phương pháp tư duy rất "cổ kính" nhưng tỏ ra có hiệu lực trong khá nhiều trường hợp, đó là tư duy, hay lập luận theo phương pháp nhân – quả.


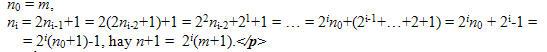

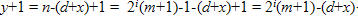
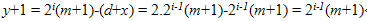
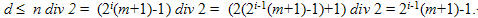
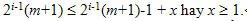
 . Từ đây suy ra B sẽ cắt dọc 2id ô từ cạnh n để tạo ra hai hình cx(n-2id) và cx2id. Từ hệ thức n+1 = 2i(c+1)+2id và i > 0 ta suy ra n-2id = 2i(c+1)-1>2ic, tức là hình cx(n-2id) có diện tích lớn hơn hình c2ic và được giao cho A. Hình này có hai cạnh x = c và y = n-2id = 2i(c+1)-1. Tương quan giữa x và y thỏa hệ thức (1), vì
. Từ đây suy ra B sẽ cắt dọc 2id ô từ cạnh n để tạo ra hai hình cx(n-2id) và cx2id. Từ hệ thức n+1 = 2i(c+1)+2id và i > 0 ta suy ra n-2id = 2i(c+1)-1>2ic, tức là hình cx(n-2id) có diện tích lớn hơn hình c2ic và được giao cho A. Hình này có hai cạnh x = c và y = n-2id = 2i(c+1)-1. Tương quan giữa x và y thỏa hệ thức (1), vì