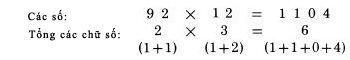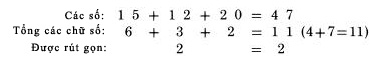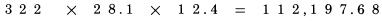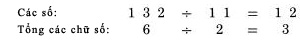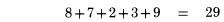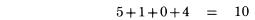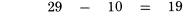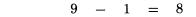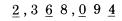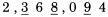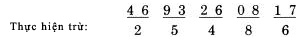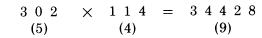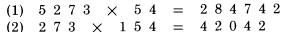Phương pháp tính tổng chữ số:

Nó cũng được gọi là phương pháp lấy phần dư cho 9. Đó là một ý tưởng cũ, được tích hợp vào hệ thống Trachtenberg. Bạn đã nhìn thấy nó trong phần kiểm tra kết quả phép cộng trước đây. Và bạn có thể vẫn nhớ, khái niệm về tổng các chữ số bao gồm:

1. Bạn tìm tổng các chữ số của một số bằng cách cộng lần lượt qua các chữ số của nó. Ví dụ, tổng các chữ số của 5,012 là 5 cộng 0 cộng 1 cộng 2 bằng 8.

2. Bạn luôn giản lược kết quả nhận được để nhận được số có một chữ số. Lấy ví dụ, tổng các chữ số của 5,012,421 là 5 cộng 0 cộng 1 cộng 2 cộng 4 cộng 2 cộng 1 là 16, rút gọn được 7.

3. Khi cộng dọc theo chiều dài số, bạn luôn bỏ qua số 9. Thực tế, nếu bạn nhìn thấy hai chữ số có tổng là 9, như 1 và 8, bạn bỏ qua cả 2 số. Do vậy, tổng các chữ số của 9,099,991 là 1, như ta quan sát được.

4. Bởi vì nguyên tắc “số 9 không được tính”, như chúng ta đã nói trong (3), tổng các chữ số ra 9 cũng tương tự như tổng các chữ số ra 0. Ví dụ, với số 513, ta thu được kết quả 0. Đó là một trường hợp đặc biệt, và bạn có thể rút gọn được nhiều thời gian nếu áp dụng.

Lấy ví dụ, bạn cần tính tổng các chữ số của 918,273,645. Bạn nên làm nó trong thời gian 3 giây, nếu bạn quan sát mà không cần tính toán. Kết quả là 0. Đó là bởi vì chúng ta bỏ qua 9, đồng thời cũng bỏ qua các cặp số có tổng là 9; và trong ví dụ này ta có các cặp số cạnh nhau kể từ sau số 9, có tổng là 9. Mọi số đều được bỏ qua, và chúng ta kết thúc với kết quả là 0.

Thông thường, các số ta làm việc thường không có các số có tổng là 9. Do vậy, bất cứ khi nào bạn cộng lại kết quả vượt quá một chữ số, rút gọn nó thành số có một chữ số bằng cách tính tổng hai chữ số của số thu được. Do đó khi ta tính tổng các chữ số của 7,288,476,588. Đầu tiên ta có 7 cộng 2 là 9, bỏ qua nó. Sau đó 8 cộng 8 là 16 là số có hai chữ số, rút gọn thành 7: 1+6 bằng 7. Tiếp tục tiến hành với 7: 7 cộng 4 bằng 11, rút gọn thành 2. Tiếp tục tiến hành với 2: 2 cộng 7 là 9, “bằng 0”, và chúng ta bắt đầu lại từ đầu. Số tiếp theo 6 cộng 5 bằng 11, “là 2” và sau đó 2 cộng 6 bằng 8; 8 cộng 8 bằng 16, “là 7”. Do đó kết quả tổng các chữ số của số trên là 7.

Các số thập phân cũng tiến hành theo cách tương tự. Chúng ta không để ý đến dấu thập phân. Với số 5.111, chúng ta cũng thu được: 5 cộng 1 cộng 1 cộng 1 bằng 8.

Giải thích:

Việc hiểu ý nghĩa của cách chúng ta đang làm không có giá trị khi thực hành, nhưng bạn sẽ thấy rất thú vị khi hiểu nó. Nguyên tắc cơ bản là: với số bạn nhận được sau khi tính toán, tổng chữ số thu gọn được của kết quả, chính xác là phần dư mà bạn nhận được khi chia nó cho 9. Lấy ví dụ, với 32. Chia nó cho 9 ta được số dư là 5. Lấy một số dài hơn, 281, khi chia cho 0 ta được thương là 31 và số dư là 2. Trong cả hai trường hợp đều bằng tổng chữ số mà ta thu được từ số ban đầu. Lưu ý chúng đều là các số có một chữ số, là phần dư của phép chia cho 9.

Áp dụng để kiểm tra:

Bây giờ chúng ta sẽ sử dụng kết quả này để kiểm tra lại các phép tính. Có vè việc áp dụng chúng sẽ khác nhau tùy thuộc vào các phép tính, nhưng chúng ta chỉ cần nhớ một nguyên tắc cơ bản chung:

Nguyên tắc cơ bản: Bất cứ khi nào bạn làm việc với các số, bạn cũng làm việc với tổng các chữ số của nó; do đó kết quả mà bạn nhận được từ tổng các chữ số của các số phải bằng với tổng các chữ số của kết quả.

Lấy ví dụ: giả sử rằng ta thực hiện phép nhân, với 92 nhân 12. Kết quả thu được là 1,104. Chúng ta viết lại nó theo ba hàng: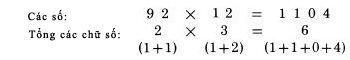

Theo nguyên tắc trên, ta nhận được tổng các chữ số của kết quả theo 2 cách. Một tính theo các chữ số nhận được từ bên trái: 2 nhân 3 là 6. Cách thứ hai là từ chính kết quả thu được: 1,104. Tất nhiên, chúng ta có 6 bằng 6, do đó kết quả được kiểm tra chính xác.

Phương pháp này cũng áp dụng kiểm tra với phép cộng: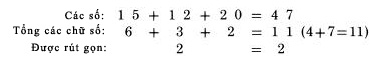

Trong ví dụ đầu ta áp dụng với phép nhân 2 số, 92 và 12, do đó ta tiến hành nhân tổng các chữ số của nó, 2 nhân 3. Trong ví dụ thứ hai, ta tiến hành cộng các số, 15 cộng 12 cộng 20, do vậy chúng ta cộng các chữ số của chúng, 6 cộng 3 cộng 2. Chúng ta luôn tiến hành thực hiện song song với phép tính, sử dụng tổng các chữ số thay vì các số đó.

Tất nhiên, các số đưa ra thường là các số lớn, có thể lên tới hàng triệu. Tuy nhiên tổng các chữ số của nó luôn là số nhỏ, được rút gọn thành số có một chữ số. Hệ quả là, việc kiểm tra chỉ cần một lượng tính toán nhỏ và đưa lại cho chúng ta giá trị xác thực công việc.

Kiểm tra với phép nhân ba số như sau: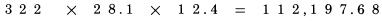

Bỏ qua dấu thập phân trong khi kiểm tra. Từ bên trái dấu bằng, chúng ta có tổng các chữ số:

Ở bên phải dấu bằng chúng ta có kết quả: 112,197.68. Tổng các chữ số của nó là 8. Do 8 bằng 8, nên chúng ta đã kiểm tra kết quả chính xác.

Trong các trường hợp đơn giản, phép chia cũng làm việc tương tự như vậy. Đây là một ví dụ: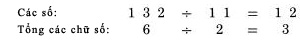

Do vậy, tổng các chữ số của kết quả là 3 (1 cộng 2), và ta cũng nhận được 3 từ phép chia ở hàng dưới, 6 chia 2. Do đó phép chia được kiểm tra đúng.

Nhưng thường xuyên, phép chia được coi là khó hơn so với hai phép tính trên vì chúng thường trả lại kết quả không là số tự nhiên. Chúng ta sẽ xem xét đến trường hợp này ở chương nói về phép chia. Tại thời điểm này, ta chỉ có thể công nhận một điều:

Phép chia có thể được kiểm tra bằng cách nhân tương ứng các tổng chữ số thu được.

Lấy ví dụ, trong ví dụ trên, chúng ta có thể nhân tổng các chữ số của thương với tổng các chữ số của số chia, 3 nhân 2. Ta được kết quả là 6, bằng tổng các chữ số của số chia, và công việc kiểm tra của ta kết thúc.

Phương pháp phần dư 11.

Thay vì tính tổng các chữ số, chúng ta có thể áp dụng một phương pháp khác như một bước kiểm tra kép, nếu việc này là cần thiết. Đó là phương pháp tính phần dư 11. Tuy nhiên chúng ta không thực hiện bất cứ phép chia nào cho 11. Cũng như nhận xét trong cách tính tổng các chữ số của một số chính là phần dư của nó khi chia cho 9, bây giờ chúng ta tính phần dư nhận được khi ta chia nó cho 11, và chúng ta tìm được cách để thực hiện nó tương tự như phương pháp trước.

TRƯỜNG HỢP ĐẦU TIÊN: VỚI CÁC SỐ CÓ HAI CHỮ SỐ

Để tìm phần dư cho 11 với các số có hai chữ số, như 48, chúng ta trừ hàng chục của nó từ hàng đơn vị: với số 48 chúng ta có 8 trừ 4 được 4. Số phần dư của 48 là 4. Đó cũng là kết quả tra nhận được khi tiến hành phép chia 48 cho 11.

Đôi khi chúng ta không thực hiện được phép trừ như vậy vì số hàng đơn vị nhỏ hơn chứ số hàng chục, như số 86. Trong trường hợp này, chúng ta tăng chữ số hàng đơn vị lên 11. Ví dụ với số 86 chúng ta có 6 cộng 11 được 17, trừ 8 được 9. Với 52 số dư 11 sẽ là 2 trừ 5, biến đổi lại thành 2 cộng 11 trừ 5 được 8.

TRƯỜNG HỢP THỨ HAI: VỚI MỌI SỐ CÓ ĐỘ DÀI LỚN HƠN HAI

Phương pháp ở đây được sử dụng với mọi chữ số thứ hai. Nói cụ thể hơn, chúng ta bắt đầu với chữ số phía ngoài cùng bên phải của số đã cho, sau đó chúng ta dịch về phía trái và cộng với các số thứ hai nhận được, tiến hành quay lại chữ số mà ta đã bỏ qua và trừ đi nó. Lấy ví dụ số 943,021,758. Chúng ta bắt đầu với số 8 ở bên phải, và lần ngược lại về bên trái cộng các số thứ hai mà ta bắt gặp: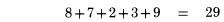

Sau đó quay lại chữ số cạnh chữ số cuối cùng, 5 và một lần nữa tiến hành cộng các số thứ hai: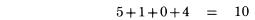

Sau đó trừ hai kết quả này: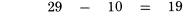

Số 19 vẫn tiếp tục được rút gọn, theo cách chúng ta đã làm với số có hai chữ số.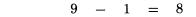

Chúng ta có phép trừ 29 trừ 10 trong ví dụ này. Giả sử trong trường hợp khác ta có phép trừ 29 trừ 35, do đó ta không thể thực hiện phép trừ, ta cũng làm tương tự như trường hợp số có hai chữ số, ta cộng 11 vào số nhỏ hơn để tăng giá trị của nó đến khi nào ta có thể trừ được. Ở đây phép trừ 29 trừ 35 trở thành 40 trừ 35 được 5.

Đối với những số trở nên lớn và không thuận tiện, như 29 và 35. Cách làm dễ dàng hơn để tránh việc thực hiện phép tính với chúng là sử dụng một thủ thuật nhỏ. Ở đây là một cách, tương tự như cách mà ta đã có lúc trước: sau khi bạn tìm được số đầu tiên, như 29, không nên tiếp tục quá trình tính với các chữ số còn lại để được 35. Thay vì vậy, bây giờ bạn nên tính với bất cứ số nào mà bạn gặp, trừ nó đi từ 29. Do vậy, trước khi bạn tính tổng các chữ số còn lại, hãy quay về với chữ số đầu tiên mà bạn tìm được từ lần tính thứ hai, chữ số bên cạnh số bên phải nhất, và trừ nó đi từ kết quả hiện thời. Tiếp tục dịch về bên trái, trừ đi các số thứ hai bắt gặp với kết quả hiện có. Thực hiện theo cách này sẽ giảm việc trừ đi tổng các số thứ hai một chút thời gian. Lấy ví dụ với số 2,368,094. Bắt đầu với số 4 ở cuối, và tính các chữ số được gạch chân: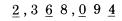

Cộng 4 với 0 là 4, cộng 6 là 10, cộng 2 là 12. Sau đó quay ngược lại với các chữ số khác: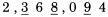

Bây giờ ta tiến hành phép trừ từ 12 cho các số này. 12 trừ 9 còn 3, sau đó trừ đi 8 – phép trừ này không thực hiện được bởi vì 8 lớn hơn 3, do đó ta tăng 3 lên 11 và đọc: 3 cộng 11 là 14 trừ 8 còn 6, trừ đi 3 còn 3. Vậy kết quả phần dư 11 là 3. Nếu bạn muốn bạn có thể trừ đi theo hướng từ phải sang trái, ta được: 12 trừ 3 được 9, trừ 8 còn 1, 1 cộng 11 là 12, 12 trừ 9 còn 3. Kết quả phần dư 11 vẫn là 3, không quan trọng cách bạn sử dụng cách làm tắt.

Một cách làm ngắn gọn khác, rất hiệu quả, đó là đi qua số đã cho sử dụng các cặp số kề nhau. Trong mỗi cặp số ta trừ một số cho số kia, bởi vì một trong số chúng là chữ số hàng chẵn và chữ số còn lại là chữ số hàng lẻ (tính chẵn lẻ dựa theo thứ tự). Lấy ví dụ, chúng ta tính với số 4,693,260,817. Viết số đã cho và nhóm các chữ số thành cặp, được biểu diễn bởi dấu gạch chân: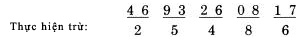

Giải thích: Ở hàng trên là các chữ số của số đã cho với các cặp số được chỉ rõ, hàng bên duới là các kết quả số dư 11 ta nhận được từ mỗi cặp, ta tính chúng theo cách thông thường bằng cách trừ hàng đơn vị cho hàng chục. Tất nhiên các cặp số được coi tạm thời như một số có hai chữ số với chữ số hàng chục và chữ số hàng đơn vị, như cặp 4 6 được coi như số 46, nhằm mục đích chỉ phải tính toán với các số nhỏ. Ta nhận được một hàng các chữ số ở dưới, mỗi số tương ứng với một cặp.

Bây giờ chúng ta cộng các số đó lại: 2 cộng 5 là 7, cộng 4 là 11, “bằng 0”, bởi vì số dư 11 của 11 là 0; sau đó cộng 8 với 6 là 14, “là 3“- giảm số thu được đi 11. Kết quả thu được cuối cùng là 3.

Áp dụng: Chúng ta áp dụng kết quả số dư 11 để tính giá trị kiểm tra, theo cách đã áp dụng với kết quả số phần dư 9 ở trước. Nguyên tắc áp dụng cũng tương tự như trước:

Bất cứ phép tính nào chúng ta thực hiện với các số, chúng ta thực hiện tương ứng với các số dư 11 cho các số đó. Sau đó kết quả thu được với các số phần dư 11 phải giống với kết quả số dư 11 thu được từ đáp số, nếu đáp số là chính xác.

Lấy ví dụ, chúng ta kiểm tra một phép nhân đã thực hiện trong chương trước. Chúng ta nhận được kết quả 302 nhân 114 bằng 34,428. Bây giờ chúng ta viết các số đó ra, mỗi số với số dư 11 tương ứng với nó ở dưới: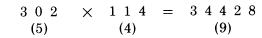

Nhân 5 với 4, kết quả sẽ là 9 trong bên phải của đẳng thức trên, nếu phép nhân là chính xác. Nó có nghĩa, tất nhiên kết quả phải bằng nhau đối với các số dư 11 của các số đã cho, là các số có một chữ số sau khi ta thực hiện quá trình rút gọn để tìm phần dư. Điêu đó đúng trong ví dụ này khi chúng ta có 5 nhân 4 được 20, trừ đi 11 còn lại 9. Chúng ta có đẳng thức bằng nhau đối với các số dư 11, 9 bằng 9, song song với phép nhân ban đầu của ta.

Đây là hai ví dụ khác. Bạn hãy xem cả hai ví dụ để kiểm tra với phương pháp trên: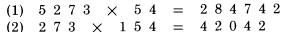

Bạn thấy rằng cả hai đều chính xác. Trong (1) chúng ta có các kết quả số dư 11 là 4 nhân 10, bằng với 7 ở bên kết quả. Rút gọn 40 bằng cách trừ 4 từ 0 (được cộng thêm 11), chúng ta thấy chính xác.

Trong (2) chúng ta kết quả phần dư 11 ở cả 2 vế cùng bằng 0; 9 nhân 0 là 0 và0 ở bên phải, do đó việc kiểm tra ra kết quả chính xác.

School@net