Cho các điểm:

x_1, x₂,…, x_N

và các giá trị tương ứng

y_1, y₂,…, y_N

Mục đích là tìm các hàm sao cho

f(x₁) = y_1, f(x₂)=y₂, …, f(x_N)=y_N

và sao cho f(x) được giả sử “hợp lý” ở những điểm dữ liệu khác. Có thể rằng một x và y được liên hệ bởi hàm f(x) ẩn danh nào đó và mục tiêu của ta là tìm ra hàm đó, nhưng định nghĩa của từ “hợp lý” phụ thuộc vào từng ứng dụng. Ta thấy rằng thường thì xác định hàm “không hợp lý” thì dễ hơn.

Khớp đường cong có ứng dụng hiển nhiên trong sự phân tích các dữ liệu thuộc thí nghiệm và còn nhiều ứng dụng khác nữa…Ví dụ, nó có thể dùng trong đồ hoạ máy tính để sản sinh ra đường cong “coi được” mà không cần pảhi lưu một số lượng lớn các điểm vẽ. Một ứng dụng có liên hệ là dùng chỉnh đường cong để cho ra một thuật giải nhanh trong tính toán giá trị của hàm chưa biết ở một điểm bất kỳ: Giữ một bảng nhỏ chứa các giá trị chính xác, sự hiệu chỉnh đường cong sẽ suy ra các điểm khác.

Bài viết này sẽ đề cập tới một trong các phương pháp cơ bản để tiếp cận bài toán này đó là phương pháp nội suy: tìm một hàm liên tục khớp với các giá trị đã cho.

Các đa thức bậc thấp là những đường cong đơn giản được sử dụng rộng rãi trong nối đường cong. Thay vì dùng các đa thức khác nhau để nối các điểm kề nhau, nối các đoạn sao cho thật mịn. Một trường hợp đặc biệt liên hệ sự tính toán tương đối trực tiếp, phương pháp này còn gọi là nội suy spline.

Spline là một thiết bị cơ học được người vẽ sơ đồ thiết kế dùng để vẽ các đường cong đẹp, có thẩm mỹ: chỉ cần xác định tập hợp các điểm (nút) rồi bẻ cong một giải plastic hay miếng gỗ linh hoạt (spline) quanh chúng và lấy vết chúng để tạo thành một đường cong. Nội suy spline thì tương đương về mặt toán học với tiến trình này và cho ra cùng một kết quả. Hình dưới minh hoạ một spline qua 10 điểm. 

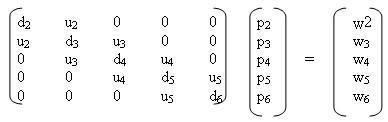
Có thể thấy rằng hình dạng của một đường cong tạo bởi spline giữa hai nút kề nhau là một đa thức bậc ba. Trở lại bài toán nối dữ liệu, điều này có nghĩa là ta nên xem đường cong là N-1 đa thức khác nhau có bậc ba.

s_i(x) = a_ix³ + b_ix²+ c_ix + d_i i = 1, 2…N-1

Với s_i(x) là đa thức bậc ba xác định giữa khoảng x_i và x_i+1. Spline có thể được biểu diễn trong một mảng bốn chiều (hay trong 4x(N-1) mảng hai chiều). Việc tạo một spline gồm việc tính các hệ số a, b,c, d từ các điểm x và các giá trị y đã cho. Việc bẻ cong một spline về mặt vật lý tương ứng với việc giải hệ phương trình với nghiệm là các hệ số. Ví dụ, Hiển nhiên ta phải có: s_i(x_i) = y_i và s_i+1(x_i+1) = y_i+1 với i = 1, 2, …, N-1 vì spline phải chạm vác nút. Không những nó phải chạm mặt toán học được này nghĩa là các đạo hàm bậc nhất của các đa thức spline phải bằng nhau ở mỗi nút (s’_i-1(x_i)= s’_i(x_i) với i=2, 3, …N-1). Thật sự thì các đạo hàm bậc hai của các đa thức cũng phải bằng nhau ở mỗi nút. Các điều kiện này cho ra 4N-6 phương trình với 4(N-1) hệ số là ẩn. Cần xác định thêm hai điều kiện nữa để mô tả tình trạng ở hai điểm cuối của spline. Có nhiều cách: dùng cái gọi là spline ‘tự nhiên’ được rút từ s”_i(x_i) = 0 và s”_N-1(x_N) = 0. Các điều kiện này cho ra một hệ đầy đủ 4N-4 phương trình với 4N- 4 ẩn số, hệ phương trình này giải được bằng phép khử Gauss với ẩn là các hệ số.

Tuy nhiên, cũng cùng một spline nhưng có thể tính toán khá hiệu quả hơn vì thật sự chỉ N-2 ẩn: hầu hết các điều kiện của spline là thừa. Ví dụ, giả sử p_i là đạo hàm bậc hai của spline tại điểm x_i, vì s”_i-1(x_i) = s”_i(x_i) = p_i với i=2, 3, …, N-1 và p_i= p_N = 0 nếu biết trước các giá trị p_i và p_N, thì tất cả các hệ số a, b, c, d có thể được tính trên các đoạn spline, vì ta có bốn phương trình với bốn ẩn số trên các đoạn: với i=1, 2, …,N-1 ta phải có:

s_i(x_i) = y_i ; s_i(x_i+1) = y_i+1 ; s”_i(x_i) = p_i ; s”_i(x_i+1) = p_i+1

Các giá trị x, y đã cho trước, để xác định đầy đủ spline chỉ cần tính các giá trị p₂, …, p_N. Để tính được, dùng điều kiện đạo hàm bậc nhất phải bằng nhau: có N-2 điều kiện ứng với N-2 phương trình cần để giải N-2 ẩn, theo p_i .Để diễn tả các hệ số các hệ số a, b, c, d theo p, các giá trị đạo hàm bậc hai, ta thay các biểu thức vào bốn phương trình trên trên mỗi đoạn spline, điều này dẫn đến một số biểu thức phức tạp không cần thiết. Thay vì diễn tả các phương trình trên từng đoạn spline ở dạng chuẩn liên hệ đến ít ẩn số hơn. Nếu ta thay các biến là t = (x-x_i)/(x_i+1-x_i) thì spline được biểu diễn như sau:

s_i(t) = ty_i+1 + (1-t)y_i + (x_i+1 -x_i)²((t³- t)p_i+1 – ((1-t)³ – (1-t)p_i)/6

bây giờ mỗi spline được xác định trên đoạn [0,1]. Phương trình này đơn giản hơn là hình thức bên ngoài của nó, vì ta chỉ quan tâm đến hai điểm nút 0 và 1 và hoặc t hoặc (1-t) bằng 0 ở những điểm mút này. Cách biểu diễn này dễ kiểm spline được nội suy và liên tục vì s_i-1(1) = s_i(0) = y_i với i = 2,…, N-1, nó chỉ hơi khó chứng minh bậc hai liên tục vì s”_i(1) = s”_i+1(0)= p_i+1. Có các đa thức bậc ba thoả những điều kiện này tại các điểm mút, vì thế chúng tương đương với các đoạn spline mô tả ở trên. Nếu ta thay thành t và tìm hệ số của x³,… thì ta sẽ có cùng biểu thức ẩn là a, b, c, d theo x, y và p giống như ta dùng phương pháp được mô tả ở đoạn trước. Nhưng không có lý do gì làm như vậy, vì ta đã kiểm rằng các đoạn spline này thoả các điều kiện cuối, và có thể lượng giá từng spline ở bất kỳ điểm nào trong đoạn của nó bằng cách tính t và dùng công thức trên (khi đã biết p).

Để tính p, ta gán các đạo hàm cấp một của các đoạn spline bằng các điểm cuối. Đạo hàm cấp 1 (theo x) của các phương trình trên là:

s’_i(t) = z_i + (x_i+1 - x_i)((3t² - 1)p_i+1– (3(1-t)² – 1)p_i)/6

Trong đó z_i= (y_i+1 - y_i)/(x_i+1 - x_i). Kế đến gán s’_i-1(1) = s’_i(0) với i = 2…N-1, ta sẽ có hệ N-2 phương trình:

(x_i-x_i-1)p_i-1 + 2(x_i+1 – x_i-1)p_i + (x_i+1 - x_i)p_i+1 = 6(z_i – z_i-1)

Hệ phương trình này thuộc dạng tam giác đơn giản dùng phép khử Gauss để giải. Ví dụ, nếu đặt u_i = x_i+1– x_i, di = 2(x_i+1 – x_i-1), và w_i = 6(z_i – z_i+1), ta có hệ phương trình với N=7:

 

Thật sự, hệ tam giác đối xứng này có nửa dưới bằng với nửa trên của đường chéo chính. Nó được xoay trên phần tử có sẵn lớn nhất nếu khong cần tìm lời giải đúng cho hệ phương trình này.

Phương pháp được mô tả ở đoạn t rên để tính spline bậc ba được dễ dàng viết dưới dạng Pascal như thủ tục makesplinedưới đây:

++++

procedure makespline;

var i: integer;

begin

readln(N);

for i:= 1 to N do readln(x[i], y[i]);

for i:= 2 to N-1 do d[i]: = 2 + (x[i+1] - x[i-1]);

for i:= 1 to N-1 do u[i]: = x[i+1] - x[i];

for i:= 2 to N-1 do

w[i]: = 6.0 * ((y[i+1) - y[i])/u[i] – (y[i] - y[i-1])/u[i-1]);

p[1]:= 0.0; p[N]:= 0.0;

for i:= 2 to N-2 do

begin

w[i+1]:= w[i+1] - w[i]* u[i]/d[i];

d[i+1]:= d[i+1] - u[i]* u[i]/d[i];

end;

for i:= N-1 downto N-1 do

p[i]:= (w[i] - u[i]*p[i+1])/d[i];

end;

+++

Các mảng d và u là đại diện matrận tam giác.

*** Mộ spline bậc ba trên N điểm có thể thực hiện theo thời gian tuyến tính.

Điều này hiển nhiên có được từ chương trình.

Ví dụ xây dựng một spline bậc ba từ năm điểm: (1.0, 2.0), (2.0, 1.5), (4.0, 1.25), (5.0,1.2), (8.0, 1.125), (10.0, 1.1).

(Các điểm trên lấy từ hàm 1+1/x). Các tham số spline tìm được bằng cách giải hệ phương trình: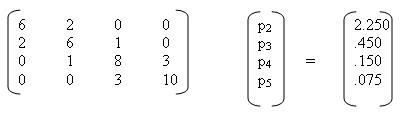

với kết quả: p₂ = 0.39541, p₃ = -0.06123, p₄ = 0.02658, p₅ = -0.00047

Để lượng giá spline cho bất kỳ giá trị x nào trong khoảng [x₁, x_N], đơn giản ta tìm khoảng [x_i, x_i+i] có chứa x, rồi tính t và dùng công thức trên cho s_i(x) (rồi dùng lại hàm này để tính p_i và p_i+1).

function eval(v: real):real;

var t: real; i: integer;

funtion f(x: real):real;

begin f:= x*x*x-x; end;

begin i:= 0;

repeat i:=i+1 until v[i+1];

t:= (u-x[i])/u[i];

eval:=t*y[i+1]+(1t)*y[i]+u[i]*(f(t)*p[i+1] + f(t-1]+f(t-1)*p[i] )/6.0;

end;

Chương trình này không kiểm tra khi v không nằm giữa x[1] và x[N]. Nếu số đoạn spline nhiều (nghĩa là N lớn) có một số phương pháp tìm có hiệu quả hơn.

School@net (Theo THNT)