Định nghĩa hoán vị:
Một hoán vị của n đối tượng được định nghĩa là một cách sắp xếp (arrangement) của n đối tượng khác nhau theo một thứ tự nào đó. mỗi thứ tự duy nhất này gọi là một hoán vị (permutation). Ví dụ có 6 hoán vị của 3 đối tượng {a,b,c} là
a b c, a c b, b a c, b c a, c a b, c b a
Các đặc tính của hoán vị là một trong tính chất quan trọng trong phân tích thuật toán (trong [1], GS Knuth đã phân tích rất nhiều điều này, các thuật toán sinh hoán vị cũng có thể tìm thấy trong chương 1 của cuốn sách kinh điển này).
Ký hiệu vòng tròn (Cycle Notations) biểu diễn hoán vị
Trong bài viết này, chúng ta coi một hoán vị c d f b e a là một sự sắp xếp của 6 đối tượng a, b, c, d, e, f (ta cũng có thể coi một hoán vị là một sự sắp xếp lại (rearrangement) hoặc đổi tên các đối tượng). Với cách giải thích này, ta có thể dùng ký hiệu 2-dòng (two-line notation), ví dụ:
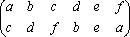 (1) (1)
có nghĩa là “a thành c, b thành d, c thành f, d thành b, e không đổi, và f thành a”. Ký hiệu 2-dòng này không bị ảnh hưởng khi ta thay đổi thứ tự cách cột, ví dụ hoán vị trên có thể viết thành:
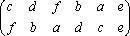
hoặc theo 718 cách tương tự.
Ký hiệu 2-dòng đôi khi không tiện lợi, và người ta thường xử dụng ký hiệu vòng tròn (cycle notation) để thể hiện điều này. Ví dụ hoán vị (1) có thể viết là:
(a c f) (b d)(2)
có nghĩa là “a thành c, c thành f, f thành a, b thành d, d thành b”. Một vòng tròn
(x1,x2, …, xn) nghĩa là “x1 thành x2, x2 thành x3, …, xn-1 thành xn, xn thành x1” với các xi đôi một khác nhau. Bởi vì ký tự e không thay đổi nên nó không xuất hiện trong ký hiệu vòng tròn này. Ký hiệu vòng tròn không phải là duy nhất, ví dụ:
(b d) (a c f), (c f a) (b d), (d b) (f a c)(3)
đều tương đương với (2). Nhưng, chú ý là ký hiệu (a f c) (b d) không tương đương vì “a thành f” là không đúng.
Thật dễ dàng để hiểu tại sao ký hiệu vòng tròn luôn luôn tồn tại. Bắt đầu với một thành phần x1 bất kỳ, hoán vị sẽ chuyển x1 thành x2, x2 thành x3, … cho đến cuối cùng (bởi vì chỉ có hữu hạn thành phần), chúng ta sẽ nhận được thành phần xn+1 nào đó là một trong các giá trị x1,…,xn trước đó. Và do đó xn+1 phải bằng x1, bởi vì nếu xn+1 bằng một trong các giá trị x2,…,xn-1 (hiển nhiên xn+1 ≠ xn) giả sử xi (2 ≤ i ≤ n-1) trong khi “xn≠ xi-1 thành xn+1=xi” (điều này là vô lý). Vậy (x1 x2 … xn) là một thành phần của hoán vị với n ≥ 1. Nếu nó chưa là một hoán vị hoàn chỉnh thì chúng ta sẽ tìm thấy một thành phần y1 và một vòng tròn khác (y1 y2 … ym) tương tự. Tất nhiên các thành phần của vòng tròn y sẽ khác vòng trõng vì nếu yi = yi, có nghĩa là xi+1 = yi+1, v.v. Và cứ như vậy cuối cùng tất cả các vòng tròn được tìm ra và ta có sự biểu diễn trọn vẹn cho hoán vị.
Một trong những ứng dụng biểu diễn hoán vị này trong lập trình đó là khi ta cần sắp xếp n đối tượng theo một thứ tự khác mà không phải dịch chuyển chúng đi đâu cả. Ví dụ để thực hiện sự sắp xếp lại (1), tức là đưa:
(a, b, c, d, e, f) (c, d, f, b, e, a)
chúng ta theo cấu trúc vòng tròn (2) và lần lượt đặt
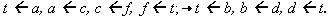
mà chỉ cần thêm một biến trung gian t mà thôi.
Nhân hoán vị (Products of permutations)
Chúng ta có thể nhân hai hoán vị với nhau, theo nghĩa của phép nhân là kết quả của một hoán vị sau hoán vị khác. Ví dụ hoán vị (1) được nhân với hoán vị
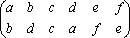
tức là ta có “a thành c, rồi thành c; b thành d, rồi thành a; c thành f, rồi thành e, …”:
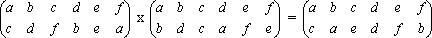 (4) (4)
Phép nhân không có tính giao hoán (commutative) tức là 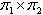 không nhất thiết phải bằng không nhất thiết phải bằng 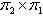 với với 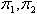 là các hoán vị. Một số ưa dùng phép nhân từ phải qua trái hơn so với các thông thường từ trái qua phải như (4). Trong thực tế, các nhà toán học luôn chia thành 2 phe trong vấn đề này (xem [1]); vậy chúng ta nên áp dụng cách biến đổi T1 rồi T2 ký hiệu bởi T1T2 hay là T2T1. Ở đây, chúng ta chọn cách T1T2. là các hoán vị. Một số ưa dùng phép nhân từ phải qua trái hơn so với các thông thường từ trái qua phải như (4). Trong thực tế, các nhà toán học luôn chia thành 2 phe trong vấn đề này (xem [1]); vậy chúng ta nên áp dụng cách biến đổi T1 rồi T2 ký hiệu bởi T1T2 hay là T2T1. Ở đây, chúng ta chọn cách T1T2.
Công thức (4) được viết dưới dạng ký hiệu vòng tròn như sau:
(a c f) (b d) (a b d) (e f) = (a c e f b)(5)
Ở đây ký hiệu “X” không cần thiết vì việc nhầm với ký hiệu vòng tròn là không có khi ta hiển nhiên thấy rằng (a c f) (b d) thực sự là tích (product) của hai hoán vị (a c f) và (b d). Phép nhân hoán vị có thể được thực hiện trực tiếp với việc biểu diễn hoán vị bởi các ký hiệu vòng tròn. Ví dụ để tính tích của một vài hoán vị sau :
(a c f g) (b c d) (a e d) (f a d e) (b g f a e)(6)
chúng ta sẽ thực hiện từ trái qua phải như sau : “a thành c, c thành d, d thành a, a thành d, và d không đổi” , kết quả cuối cùng là “a thành d”, ta viết “(a d” là lời giải thành phần của hoán vị cần tìm. Giờ ta xét tiếp thành phần d: “d thành b thành g”, ta lại có “(a d g” và tiếp tục với g ta có “g thành a thành e thành f thành a”, như vậy vòng tròn đầu tiên sẽ là “(a d g)”. Ta lại tiếp tục với một thành phần mới chưa xuất hiện c, và tương tự tìm được vòng tròn (c e b). Như vậy ta có hoán vị của (6) là (a d g) (c e b).
Đặc tả thuật toán nhân hoán vị bởi ký hiệu vòng tròn
Sau đây chúng tôi trình bày một thuật toán đơn giản thực hiện phép nhân hoán vị được biểu diễn bởi ký hiệu vòng tròn này. Đầu vào của thuật toán là tích các vòng tròn (như (6)) và tính ra kết quả dưới dạng tích các vòng tròn rời nhau (disjoint cycles). Để đơn giản ở đây chúng tôi không trình bày việc loại bỏ (removal) các vòng tròn đơn (singleton cycles: ví dụ (e), thủ tục đơn giản này có thể giành cho bạn đọc). Như ví dụ trên đã trình bày phần nào hoạt động của thuật toán, chúng ta lần lượt “đánh dấu” (tạm dịch từ từ tag trong nguyên văn thuật toán được trình bày trong [1]) các thành phần của công thức đầu vào.
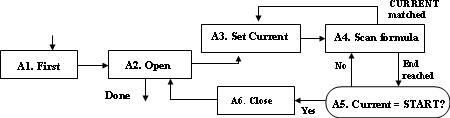
A1. [First pass] Đánh dấu tất cả các dấu ngoặc đơn (parenthese) bên trái, và thay thế mỗi dấu ngoặc đơn bên phải bởi một sao chép đã được đánh dấu của ký hiệu đầu vào sao cho nó theo dấu ngoặc đơn bên trái thích hợp (xem ví dụ bảng dưới)
A2. [Open] Tìm kiếm từ trái qua phải, tìm các thành phần chưa đánh dấu (untagged) đầu tiên của đầu vào. (Nếu tất cả các thành phần đã được đánh dấu, thuật toán kết thúc). Đặt START bằng thành phần tìm được và đưa ra một dấu ngoặc trái và thành phần đó, đồng thời đánh dấu nó.
A3. [Set CURRENT] Đặt CURRENT bằng thành phần tiếp theo của công thức.
A4. [Scan formula] Thực hiện qua phải cho đến khi hoặc gặp thành phần kết thúc của công thức hoặc tìm được thành phần bằng với CURRENT; trong trường hợp thứ hai, đánh dấu nó và trở về bước A3.
A5. [CURRENT=START?] Kiểm tra, nếu CURRENT START, đưa ra CURRENT và trở lại bước A4 một lần nữa tại bên trái của công thức (bằng cách đó tiếp tục hoàn thành vòng tròn của công thức đầu ra).
A6. [Close] Lúc này một vòng tròn hoàn chỉnh của công thức đầu ra đã được tìm thấy. Đưa ra một dấu ngoặc phải và trở lại bước A2.

| After Step |
START |
CURRENT |
(a c f g) |
(b c d) |
(a e d) |
(f a d e) |
(b g f a e) |
Output |
| A1 | | | (a c f g a) | (b c d b) | (a e d a)
| (f a d e f) | (b g f a e b) | |
| A2 | a | | (a c f g a) | (b c d b) | (a e d a) |
(f a d e f) | (b g f a e b) | (a |
| A3 | | | (a c f g a) | (b c d b) | (a e d a)
| (f a d e f) | (b g f a e b) | |
| A4 | | | (a c f g a) | (b c d b) | (a e d a)
| (f a d e f) | (b g f a e b) | |
| ... | | | | | | | | |
| A4 | a | d | | | | | | |
| ... | | | | | | | | |
| A4 | a | a | | | | | | |
| ... | | | | | | | | |
| A5 | a | d | | | | | | |
| ... | | | | | | | | |
| A5 | a | g | | | | | | |
| ... | | | | | | | | |
|
A5 |
a |
a
|
|
|
|
|
|
|
|
A6 |
a |
a
|
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
|
|
|
A2 |
c |
a |
|
|
|
|
|
|
| ... |
|
|
|
|
|
|
|
| | A5 | c | e |
|
|
|
|
|
| | ... |
|
|
|
|
|
|
|
| | A5 | c | b |
|
|
|
|
|
| | ... |
|
|
|
|
|
|
|
| | A6 | c | c |
|
|
|
|
|
| | ... |
|
|
|
|
|
|
|
| |
A6 | f | f |
|
|
|
|
| |
 là ký hiệu biểu diễn con trỏ theo sau phần tử vừa quét (scan), các thành phần được đánh dấu có màu xám mờ hơn. là ký hiệu biểu diễn con trỏ theo sau phần tử vừa quét (scan), các thành phần được đánh dấu có màu xám mờ hơn.
Minh họa với công thức (6). Bảng trên đây diễn tả các bước thực hiện của thuật toán. Dòng đầu tiên của bảng là công thức sau khi ký hiệu ngoặc phải đựoc thay thế bởi thành phần đầu tiên của vòng tròn tương ứng; các dòng tiếp theo thể hiện quá trình thực hiện của thuật toán và lần lượt thêm các thành phần được đánh dấu. Một con trỏ (cursor) thể hiện biến chạy trong công thức.
Kết quả thuật toán là (a d g) (c e b) (f); chú ý là các vòng tròn đơn sẽ có thể xuất hiện trong công thức đầu ra và không khó để sử dụng thủ tục loại bỏ nó.
Như vậy, bài viết đưa ra một ký hiệu biểu diễn hoán vị khá thú vị ứng dụng trong lập trình, và đưa ra thuật toán ứng dụng trên bài toán nhân hai hoán vị. Mong bài viết có ích cho một số ứng dụng thuật toán mà các bạn gặp phải trong học tập.
Tài liệu tham khảo
1. GS Knuth (ĐH Stanford, Hoa Kỳ), Nghệ thuật lập trình, tập 1, 1997.
2. Từ điển Wikipedia tiếng Anh (en.wikipedia.com)
Đinh Quang Huy(huydq@coltech. (Theo Tạp chí Tin học và Nhà trường)
|

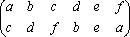 (1)
(1)
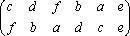
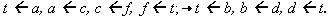
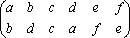
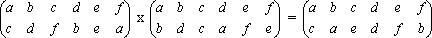 (4)
(4)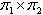 không nhất thiết phải bằng
không nhất thiết phải bằng 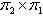 với
với 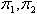 là các hoán vị. Một số ưa dùng phép nhân từ phải qua trái hơn so với các thông thường từ trái qua phải như (4). Trong thực tế, các nhà toán học luôn chia thành 2 phe trong vấn đề này (xem [1]); vậy chúng ta nên áp dụng cách biến đổi T1 rồi T2 ký hiệu bởi T1T2 hay là T2T1. Ở đây, chúng ta chọn cách T1T2.
là các hoán vị. Một số ưa dùng phép nhân từ phải qua trái hơn so với các thông thường từ trái qua phải như (4). Trong thực tế, các nhà toán học luôn chia thành 2 phe trong vấn đề này (xem [1]); vậy chúng ta nên áp dụng cách biến đổi T1 rồi T2 ký hiệu bởi T1T2 hay là T2T1. Ở đây, chúng ta chọn cách T1T2.

 là ký hiệu biểu diễn con trỏ theo sau phần tử vừa quét (scan), các thành phần được đánh dấu có màu xám mờ hơn.
là ký hiệu biểu diễn con trỏ theo sau phần tử vừa quét (scan), các thành phần được đánh dấu có màu xám mờ hơn.

